Elements and Atoms

In AP® Chemistry, an element is a substance made up of specific atoms. Each atom is composed of electrons, neutrons, and protons. Neutrons and protons are in the nucleus of the atom while electrons reside in the space around the nucleus. The number of protons in an element signifies its atomic number and determines the characteristics of the element. The particles inside the nucleus indicate the mass number of an element. The mass number is the sum of protons and neutrons in an atom. An element is represented as in the image below.

	A = Mass number = 12
	Z = Atomic number = 6
	Protons = Z = 6
	Neutrons = A-Z = 12 – 6 = 6
	Electrons = Protons = 6

Table 1: Element Notation: Carbon-12

The element carbon has an atomic number (Z) of 6. In carbon’s stable state, its mass number (A) is equal to 12. Using the definition of mass number, the number of neutrons in carbon-12 is equal to 12-6 = 6. The number of electrons is the same as the number of protons for neutral elements (in this case, 6).

Defining Isotopes

Isotopes are atoms with the same number of protons but a different number of neutrons. Since the number of protons determines the element, isotopes are the same elements with different mass numbers. Each element in the periodic table has isotopes, some of which have multiple forms. The isotopes of an element have nearly identical properties. Chemical properties depend on the electron structure, which is the same for different isotopes of the same element; however, heavier isotopes react more slowly compared to lighter isotopes of the same element. Meanwhile, the physical properties of isotopes differ because of the difference in their masses. The significance of different isotopes of an element corresponds to its nuclear stability.

Radioactivity of Isotopes

The stability of an isotope depends mainly on its neutron-proton ratio. This ratio increases with increasing atomic number. An isotope with an almost equal number of neutrons and protons has at least one stable nuclide. Elements up to calcium have stable isotopes. Unstable isotopes undergo radioactive decay. Isotopes that undergo radioactive decay are also called radioisotopes. Radioactive decay (sometimes referred as radioactivity or nuclear decay) is the emission of radiation of an unstable atom. Radiation is emitted in the form of alpha particles, beta particles, and gamma rays. In reviewing AP® Chemistry, we can use the belt of stability to identify the type of radiation an isotope will likely undergo.

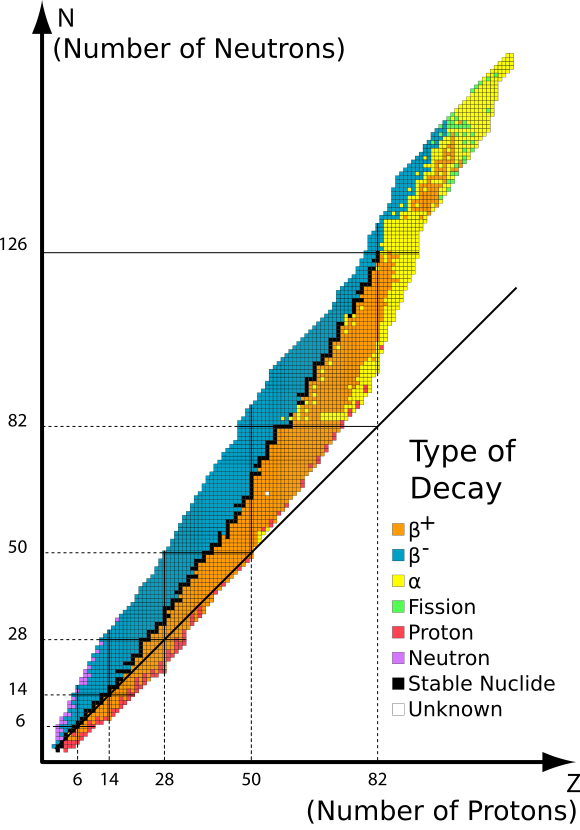
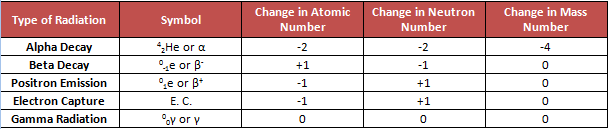
Black zigzag lines represent the belt or band. They are stable nuclides of elements. Elements located on the upper right of the band undergo alpha decay. Alpha decay decreases both the proton and neutron number by two. Alpha decay corresponds to the release of the helium nucleus, _{ 2 }^{ 4 }{ He }, equivalent to an alpha particle (\alpha). On the left of the belt are the elements that undergo beta decay. Beta decay is the emission of a beta particle (\beta^-). This radioactivity is also the same as the addition of a proton to the isotope. The elements below the belt of stability in the orange region undergo positron (\beta^+) emission or electron capture. Sometimes, an isotope will undergo different kinds of radioactive decay until the nuclide becomes stable. These different radiations are summarized in the table below to easily answer questions in AP® Chemistry.

Isotope Notation

As mentioned earlier in this discussion, isotopes have the same number of protons but a different number of neutrons. In AP® Chemistry, atomic number and mass number are indicated as subscript and superscript, respectively. Since isotopes are from the same element, the atomic number is usually left off. There are two ways of naming isotopes. They can be named with a chemical formula of an element with the mass number as a superscript to the left of the element. Isotopes can also be named by using the element name followed by the mass number. For example, another isotope of carbon has 8 neutrons and 6 protons. This specific isotope of carbon has a mass number of 14. This isotope is named _{ }^{ 14 }{ C} or carbon-14.

Abundance of Isotopes and Atomic Mass

Aside from stability, another difference in isotopes is the abundance of each isotope in the environment. The abundance of an isotope is given as a percentage of the total number of isotopes of the same element. This means that each element has a total abundance of 100\%, and the total is subdivided for different isotopes. We need to know the abundance of isotopes to calculate the atomic mass of an element.

To calculate the average atomic mass of an element, every isotope of that element is considered. The percent abundance of each isotope is multiplied by its corresponding mass number. The average atomic mass is the sum of the products of all isotopes of the element.

We can use the element chlorine as an example. Chlorine has two isotopes. 75.77\% of chlorine atoms are composed of an isotope with 18 neutrons. The remaining chlorine has an isotope with 20 neutrons. Calculate the average atomic mass of chlorine, given that the atomic number of chlorine is 17.

To properly write out the solutions for AP® Chemistry calculations, we need to provide the given data in the problem. These are:

Chlorine: atomic number = 17

Isotope 1: abundance = 75.77\%; neutrons = 18

Isotope 2: neutrons = 20 neutrons

In the problem, we are looking for the atomic mass of chlorine.

We know that the atomic number of an element is the same as the number of protons in that element. Calculating the mass number of each isotope, we have:

\text{Isotope 1: mass number = neutrons + protons} = 18 + 17 = 35 \text{ amu}

\text{Isotope 2: mass number = neutrons + protons} = 20 + 17 = 37\text{ amu}

Now, we can identify the isotopes. Isotope 1 is chlorine-35, and Isotope 2 is chlorine-37.

Noting that an element has 100\% abundance, we can get the abundance of chlorine-37.

\text{Abundance} = 100\% - 75.77\% = 24.23\%

We need to change these percents of abundance to their decimal forms and multiply them by the mass number of their respective isotopes. The sum will be the average atomic mass of the element.

\text{Average atomic mass = (abundance) (mass number) + (abundance) (mass number)}

\text{Average atomic mass} = (0.7577) (35 \text{ amu}) + (0.2423) (37\text{ amu})

\text{Average atomic mass} =35.48 \text{ amu}

The average atomic mass is the listed atomic weight of the element in the periodic table. Chlorine has an atomic weight of 35.48\text{ amu}.

Isotope Separation

Isotopes have significant applications in different fields. A great deal of attention is given to finding ways to concentrate certain isotopes. Since isotopes of the same elements have nearly the same chemical properties, some elements can be separated by physical means. Practical separation of isotopes includes diffusion, centrifugal separation, mass spectrometry, use of lasers, distillation, and chemical methods.

In diffusion, separation occurs because of the difference in the isotopes’ velocities. Lighter isotopes diffuse more quickly through a membrane. The difference in the travel rate of isotopes is proportional to the square root of their mass. This means achieving purity is difficult. Many stages or cascades are needed in the process. The first large-scale separation of uranium isotopes was done using diffusion.

Centrifugal separation of isotopes utilizes centrifugal force and the difference in the masses of isotopes. Materials are rotated rapidly in a circular motion, causing heavier isotopes to move towards the outer wall. Fewer stages or cascades are used compared with the process of diffusion. Centrifugal separation is the main method used globally in the purification of uranium. UF_6 is placed in a cylinder that undergoes high-speed rotation. Heavier gas molecules containing U-238 collect on the sides of the wall. Molecules mainly composed of U-235 in the center are passed to the next stage.

Mass spectrometry uses an electromagnetic field to achieve isotope separation. Charged particles are deflected by the magnetic field. The amount of deflection depends on the mass of the particles. A large amount of energy is required for mass spectrometry, making this process impractical for large-scale separation.

Light amplification by stimulated emission of radiation (laser) is used to excite an isotope of an element. The absorption of light is dependent on the particle’s mass. The ionized atoms are removed with the use of an electric field. This process is still not used extensively, but it gets a lot of attention since this method may be cheaper and easier compared to other processes of isotope separation.

Cryogenic distillation is the process by which isotopes are cooled to their liquefaction temperature in tall columns. Heavier isotopes sink and lighter isotopes float, allowing for the collection of isolated isotopes.

Some isotopes are separated by the difference in their reaction rates. This chemical method of separation is used mainly for hydrogen. Hydrogen has three naturally occurring isotopes, and these isotopes have different chemical properties. Protium is an isotope of hydrogen with no neutron. Deuterium has one neutron and tritium has two neutrons. Lighter isotopes react more quickly compared to heavier isotopes, allowing for this separation process. Heavy water, or water with deuterium as its hydrogen, is produced in large scale using this process.

Application of Isotopes

Isotopes have applications in the fields of medicine, environmental science, agriculture, food preservation, archaeology, and production of energy.

Some applications of isotopes in the medical field include evaluation of a disease, treatment of a disease, and production of medical instruments. Nuclear medical imaging is widely used in identifying medical conditions at an early stage. Isotopes used in nuclear imaging are fluorine-18, gallium-67, rubidium-82, nitrogen-13, and more. Erbium-169 is used in relieving arthritis pain. Cobalt-60 is used to damage cancer cells without undergoing surgery. Skin cancer is treated with phosphorus-32 and strontium-90. Plutonium-238 is used in the nuclear batteries of pacemakers.

Agricultural use of isotopes includes pest control and soil fertility investigation. Phosphorus-32 is used to track the intake of fertilizers from roots to leaves. Beta-radiation is used to map the usage of phosphorus. Nitrogen-15 is used to determine the effectiveness of fertilizers on the growth of plants.

As we know, radioactivity is used to determine the age of a substance. This method is called radioactive dating and is based on the half-life of each element. Carbon-14 is the most commonly used isotope in this application. The use of carbon is limited to organic materials. In AP® Chemistry, there are problems that involve determining the age of a substance, given its composition.

Gamma rays from cobalt-60 are used to kill bacteria in food without changing the quality of food, making the food last longer. Sodium-24 is used in measuring engine deterioration. Plutonium is used in nuclear reactions to produce electrical energy and nuclear weapons. There are many more applications of isotopes not mentioned in this section.

Radioactive Dating Calculations

Radioactive decay undergoes a first-order reaction. There are different types of problems involved in the kinetics of radioactive decay. These problems include the calculation of the rate decay constant, the original amount of the sample, the remaining amount of the sample, the age of the sample used, and the determination of the sample’s half-life. If carbon-14 is the element involved, its half-life is 5720 \text{ years}. Formulas used in the calculations are:

ln \dfrac{N}{N_0} = -kt

t_{1/2} = \dfrac{ln 2}{k}

…where N = amount of substance in the sample after time, t; N_0 = initial amount of substance in the sample; k = rate decay constant; t = time elapsed (age of the sample); and t_{1/2} =half-life of the element.

Sample Problems:

1. Calculation of remaining amount of sample:

Determine the amount of a 2 \text{ g} sample that will remain after 20 \text{ min} if the decay rate constant is equal to 0.15 \text{ min}^{-1}.

ln \dfrac{N}{2 \text{ g}} = -(0.15 \text{ min}^{-1})(20 \text{ min})

ln \dfrac{N}{2 \text{ g}} = -0.30

\dfrac{N}{2 \text{ g}} = e^{-0.30} = 0.741

N = 1.48 \text{ g}

2. Calculation of rate decay constant:

Solve for the decay rate constant if 70\% of the original sample remains after 20 \text{ hr}.

ln \dfrac{70}{100} = -k(20 \text{ hr})

-0.357 = -k(20 \text{ hr})

k= 0.018 \text{ hr}^{-1}

3. Calculation of original amount of sample used:

A sample has a mass of 450 \text{ g} after 2 \text{ hr}. What is the initial amount of the sample given that the rate constant is equal to 0.056 \text{ hr}^{-1}.

ln \dfrac{450 \text{ g}}{N_0} = -(0.056 \text{ hr}^{-1})(2 \text{ hr})

ln \dfrac{450 \text{ g}}{N_0} = -0.112

\dfrac{450\text{ g}}{N_0} = e^{-0.112} = 0.894

N_0 = 503 \text{ g}

Let’s put everything into practice. Try this AP® Chemistry practice question:

Looking for more AP® Chemistry practice?

Check out our other articles on AP® Chemistry.

You can also find thousands of practice questions on Albert.io. Albert.io lets you customize your learning experience to target practice where you need the most help. We’ll give you challenging practice questions to help you achieve mastery of AP® Chemistry.

Start practicing here.

Are you a teacher or administrator interested in boosting AP® Chemistry student outcomes?

Learn more about our school licenses here