Timeline of the Atomic Theory
Before we discuss quantum numbers and theory, we need to briefly review how we arrived at the current atomic theory (Quantum Theory and the Bohr Model).
The Rutherford Model
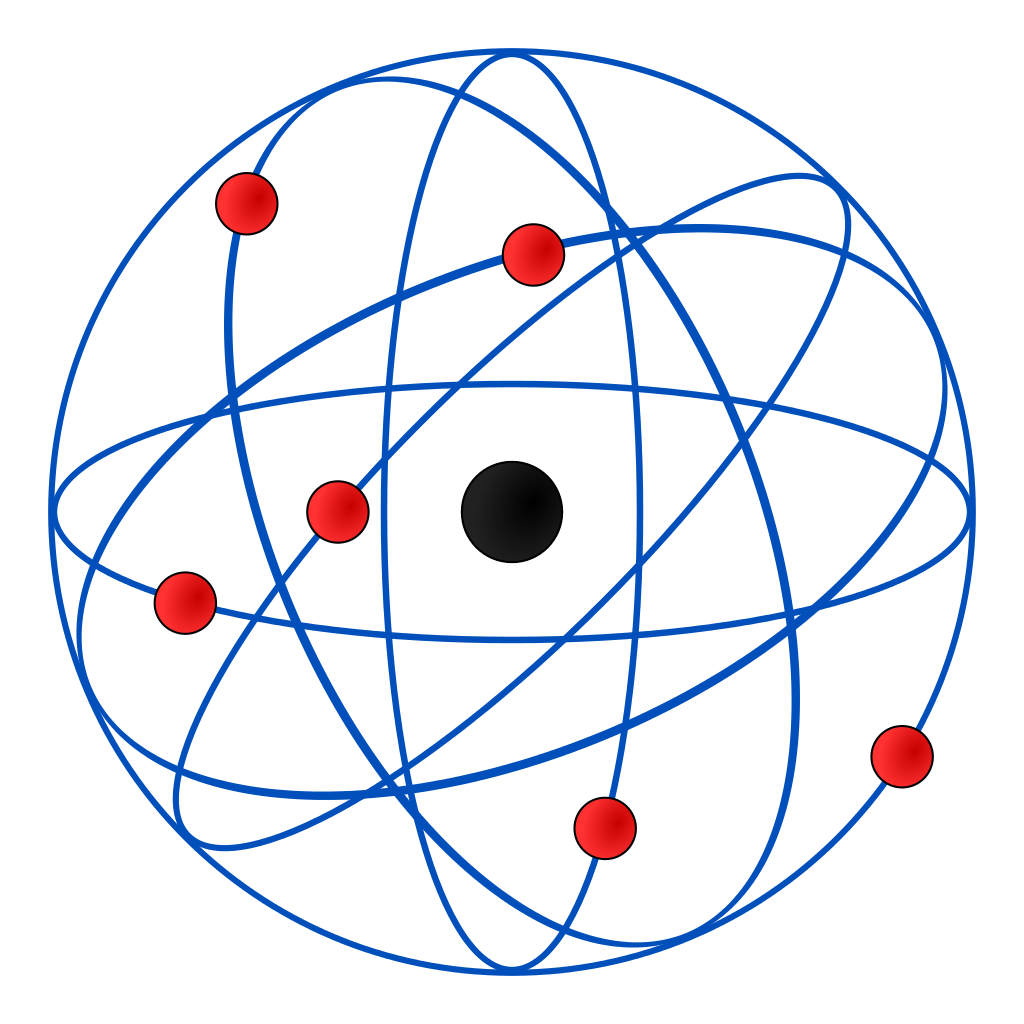
Rutherford proposed that an atom was made up of a dense, positive nucleus, surrounded by mostly empty space and negative electrons. Rutherford’s model of the atom prevailed for many years until scientists started noticing inconsistencies. Physics established that an electron moving in a curved path around a nucleus must give off energy. As it continuously loses energy, the electron should spiral into the nucleus. Since this does not happen, there needed to be a new model to describe atoms.
The Bohr Model
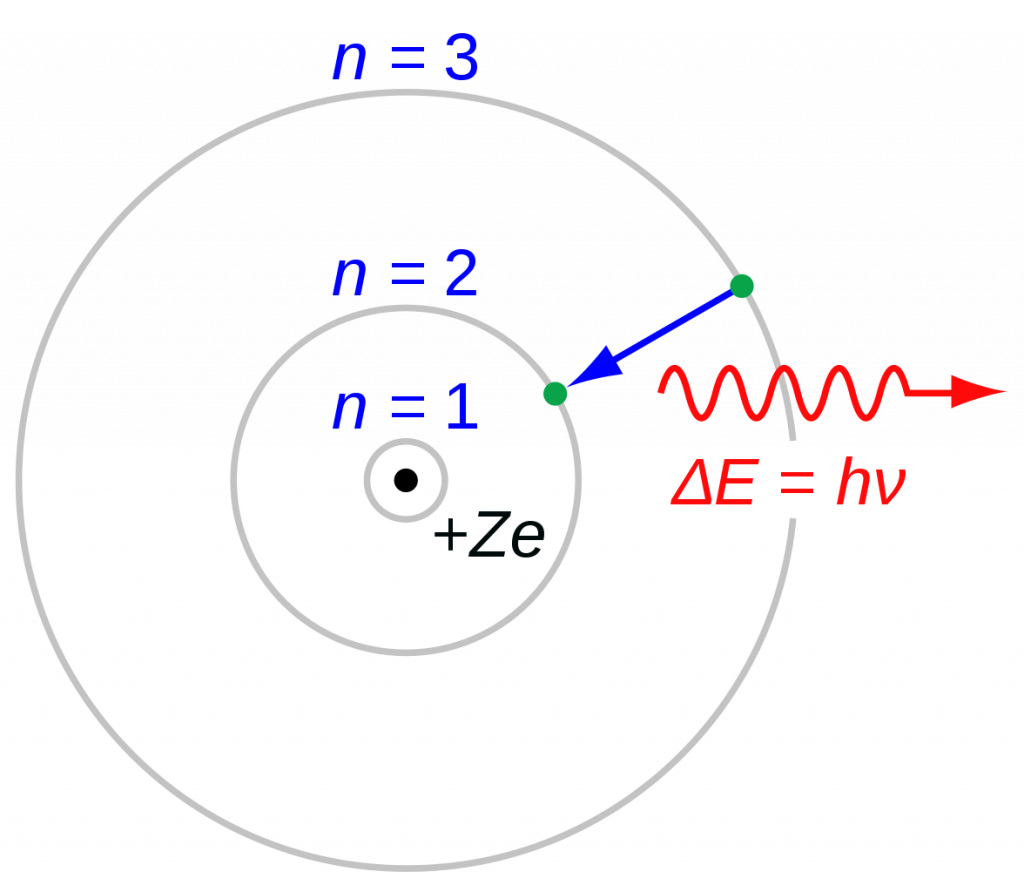
Bohr proposed that the nucleus is in the center with protons and neutrons, and the electrons are around the nucleus, but instead of orbiting in circles, he thought that they exist in distinct energy levels in spheres, accounting for the specific changes in light emitted as electrons gained energy (photons).
Bohr proposed his theory after observing electrons transition between energy states using a hydrogen discharge lamp. The Bohr model states that as an electron moves between energy levels, energy is emitted or absorbed as a photon. This causes a difference in the frequency and wavelength of the light viewed through the element being observed, as electrons absorb or emit photons.
The Bohr model was successful in modeling the activity of a hydrogen atom, but it was not accurate with other atoms. Several changes were made, and in current models, electrons still have discrete energies, but they also occupy specific orbitals. These are specifically shaped areas in which an electron may exist but are not actually visible outside of computer modeling. This has given us our current understanding explained using quantum numbers and theory.
Quantum Numbers and Theory
To describe the location of an electron in an element, we utilize quantum numbers and theory. Each electron is described using four different quantum numbers, and no two electrons in the same atom can have the same set of numbers. The numbers indicate the shell, subshell, orbital, and spin of the electron. This tells you all of the characteristics of any given electron in an atom.

The first number is the principal quantum number, represented by n. The principal quantum number tells you what shell the electron is in.
An electron’s n tells you:
• its approximate distance from the nucleus
• the size of the orbital it is in
• its energy level
The larger n is, the larger the atom is. The values of n are all positive integers (beginning with 1) because they represent shells, and there will always be at least one shell in an atom. The first of which is n=1 and is the lowest energy shell. According to the quantum theory, this shell is the closest to the nucleus.
When an electron moves from a less stable position to a more stable position, it moves from a higher energy position to a lower energy position, making this a favorable and common change. The wavelength and frequency of the photon emitted depend on the energy change of the electron. For example, as an electron falls from n=3 to n=2 (a higher energy state to a lower energy state), it emits (releases) red light (photons at 450-495 wavelengths), but when an electron falls from n=6 to n=2, violet light is emitted.
As an electron is excited (from “absorbing” photons or energy), it can jump to a higher energy level, increasing the n value by a whole number. When an electron “emits” energy, it jumps to a lower energy level, decreasing the n value by a whole number. So, n=4 has more energy than n=3. As an electron gains energy, it jumps to a higher energy level, absorbing photons, and increasing n.
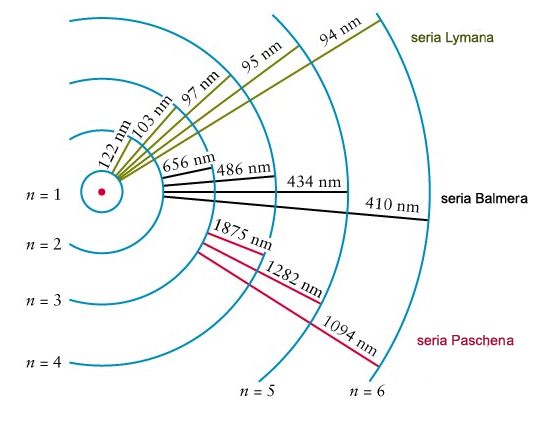
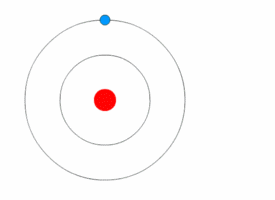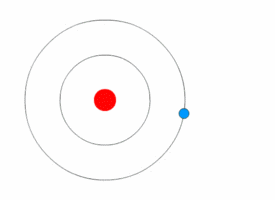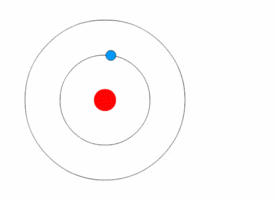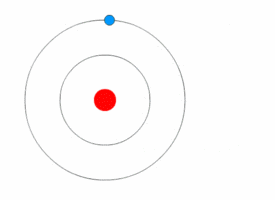
Examples:
1. If an electron’s principal energy level goes from n=5 to n=4, it has moved to a lower energy level, so it has emitted (lost) energy as a photon.
2. If you have two atoms, one with n=3 and the other n=4, the atom that is n=4 has more energy because it has a higher n and is larger (because atomic radius increases with n).
3. When an electron moves from n=2 to n=4, it has moved to a higher energy level, so it is absorbing energy as photons.
Key Concept: Electrons exist in specific energy levels called shells. When electrons change energy levels, they absorb or emit energy as photons.
Subshells
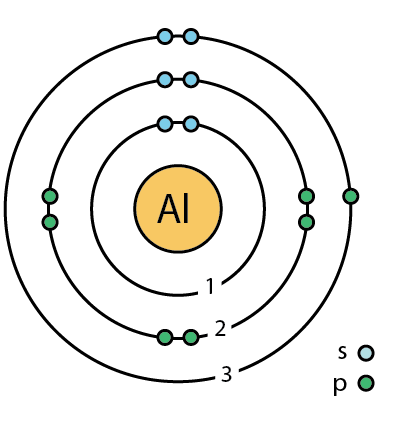
The next part of quantum numbers and theory is the orbital angular momentum quantum number and the idea of subshells. The orbital angular momentum quantum number, l, tells you the subshell in which the electron exists. This tells you the shape of the subshell the electron is in. This is also always a whole number, but ranges from 0 to n-1, meaning it can never be larger than n.
| n | l |
| 1 | 0 |
| 2 | 0, 1 |
| 3 | 0, 1, 2 |
| 4 | 0, 1, 2, 3 |
Each l number correlates to a specific subshell. The most common of these subshells are labeled s, p, d, and f.
| l | Subshell |
| 0 | s |
| 1 | p |
| 2 | d |
| 3 | f |
This means that n = 1 has one subshell, an s; n=2 has two subshells, one s and one p; n=3 has three subshells, one s, one p, and one d.
| n | Subshells Present |
| 1 | s |
| 2 | s, p |
| 3 | s, p, d |
| 4 | s, p, d, f |
The shape of the subshell is determined by its energy level. Every type of subshell (s, p, etc.) has a specific shape.
An s orbital is spherical around the nucleus. Think of the inside of a jawbreaker. The center is the nucleus. The next layer around it is the 2s subshell. The next layer is 3s, and so on. A p orbital is shaped like a dumbbell. See the image below for the shapes of each type of orbital in each subshell. All of the orbital shapes in one box combine to form that subshell.
Quantum numbers and theory begin to get very complicated when you try to memorize the shapes. Don’t worry about that — just remember that s orbitals are spheres, p orbitals are dumbbells, d orbitals are two balloons connected at the ends by a donut, and f orbitals look like flowers.
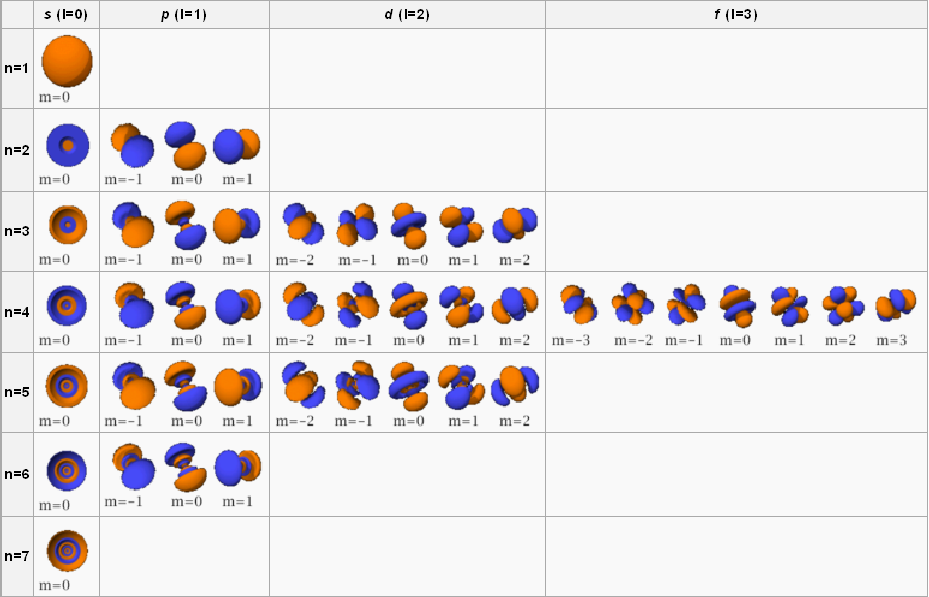
To view these, imagine that they are on a three-dimensional plane, as in the image below.
Subshells have names composed of the principal quantum number and the letter of the subshell. If an electron is in the p subshell (l = 1) of the third principal energy shell (n = 3), it is in the 3p subshell.
Examples:
1. If an electron has n=4 and l = 0, it is in the 4s subshell.
2. If an electron is n=3, it could have three possible subshells: 3s, 3p, and 3d, because l= 0, 1, and 2.
Key Concept: Every energy level (shell) has subshells, each of which has a specific shape.
Orbitals
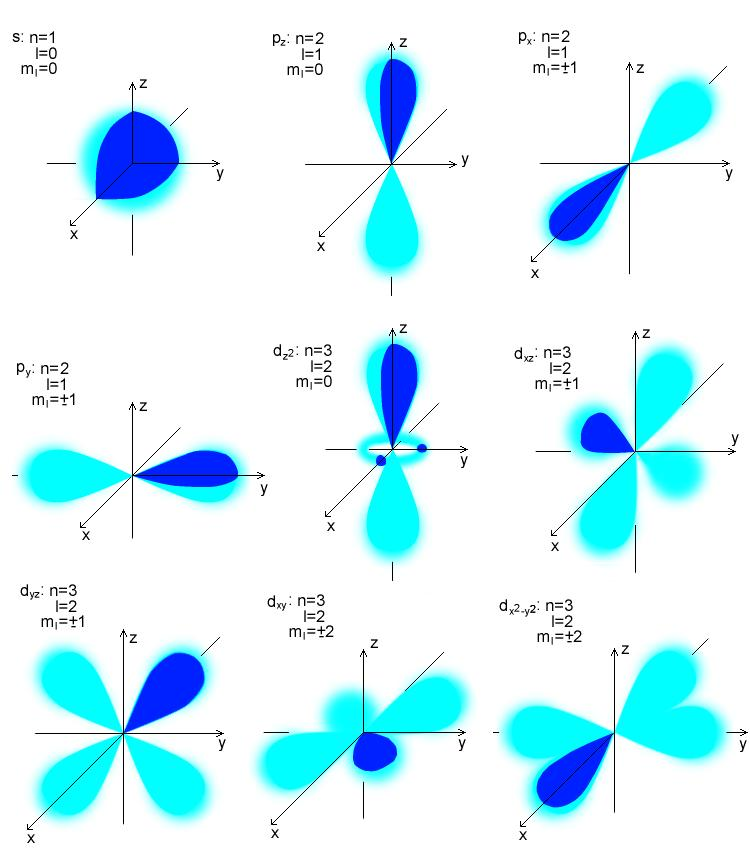
Every subshell has orbitals. The number of orbitals is determined by the size of the subshell. Each subshell of the same type has the same number of orbitals.
The magnetic quantum number, m_l, tells you the orbital the electron is in and describes the energy levels in its subshell. The values of m_l are again whole numbers, ranging from -l to +l. So if l = 2, them_l values are -2, -1, 0, 1, and 2. This means that when l = 2, there are five possible orbitals for an electron to occupy.
| Subshell | l | Possible m_l Values | Number of Orbitals |
| s | 0 | 0 | 1 |
| p | 1 | -1, 0, 1 | 3 |
| d | 2 | -2, -2, 0, 1, 2 | 5 |
| f | 3 | -3, -2, -1, 0, 1, 2, 3 | 7 |
Key Concept: The number of orbitals is different for each subshell and every subshell of a single type will have the same number of orbitals.
Electron Spins
Finally, the electron spin quantum number, m_s, tells you the electron spin. Who would have guessed?
Each orbital can hold two electrons. The two electrons have opposite spins, which we have arbitrarily called up and down. This up or down spin is represented by +\dfrac{1}{2} and -\dfrac{1}{2} or an “up arrow” and “down arrow”, as seen below.
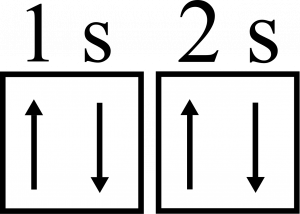
In this image, you also see that the orbital is represented by a box. Each box can hold two electrons. Each subshell has a different number of orbitals, which can be represented by multiple boxes, as seen below:
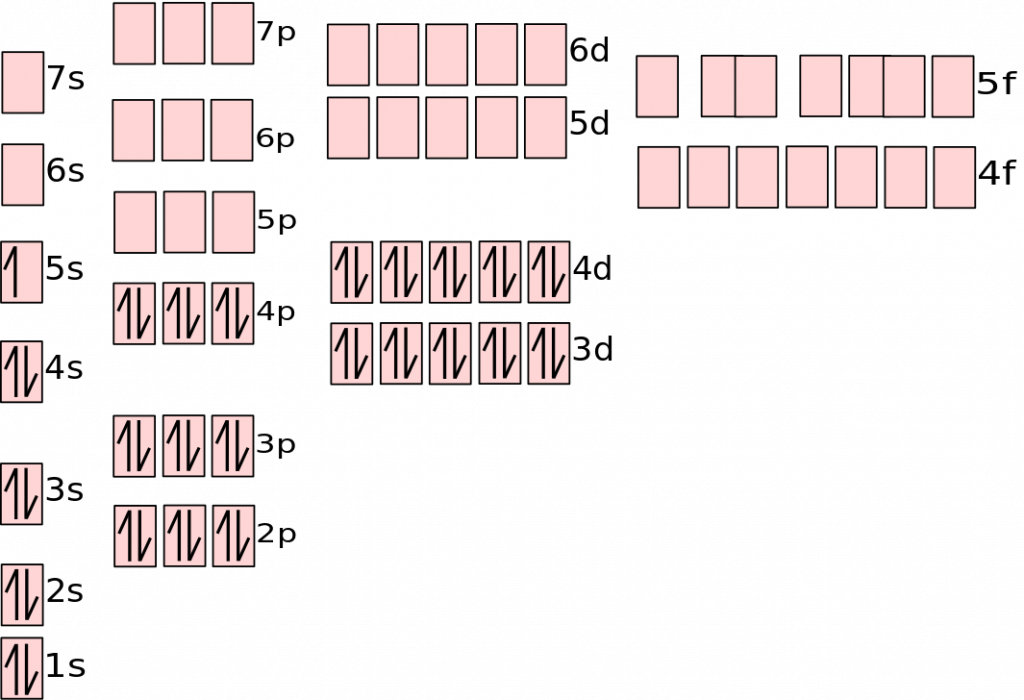
This is an example of the electron configuration for silver. Notice that each orbital only has two electrons. The s subshell has one orbital, the p has three, the d has five, and the f has seven. This is another way of demonstrating the locations of the electrons in an atom. See the review for electron configuration for more information on this type of diagram.
Example:
For an electron that is n=2, l=1, and m_l=0, there are two possible quantum number configurations. Since the magnetic quantum number is given, you only have two options, the positive and negative spins. So the two possible configurations are n = 2, l = 1, m_l = 0, m_s =-\dfrac{1}{2} and n = 2, l = 1, m_l = 0, m_s =\dfrac{1}{2}.
Key Concept: Each atomic orbital can hold two electrons with opposite spins.
Ionization Energy
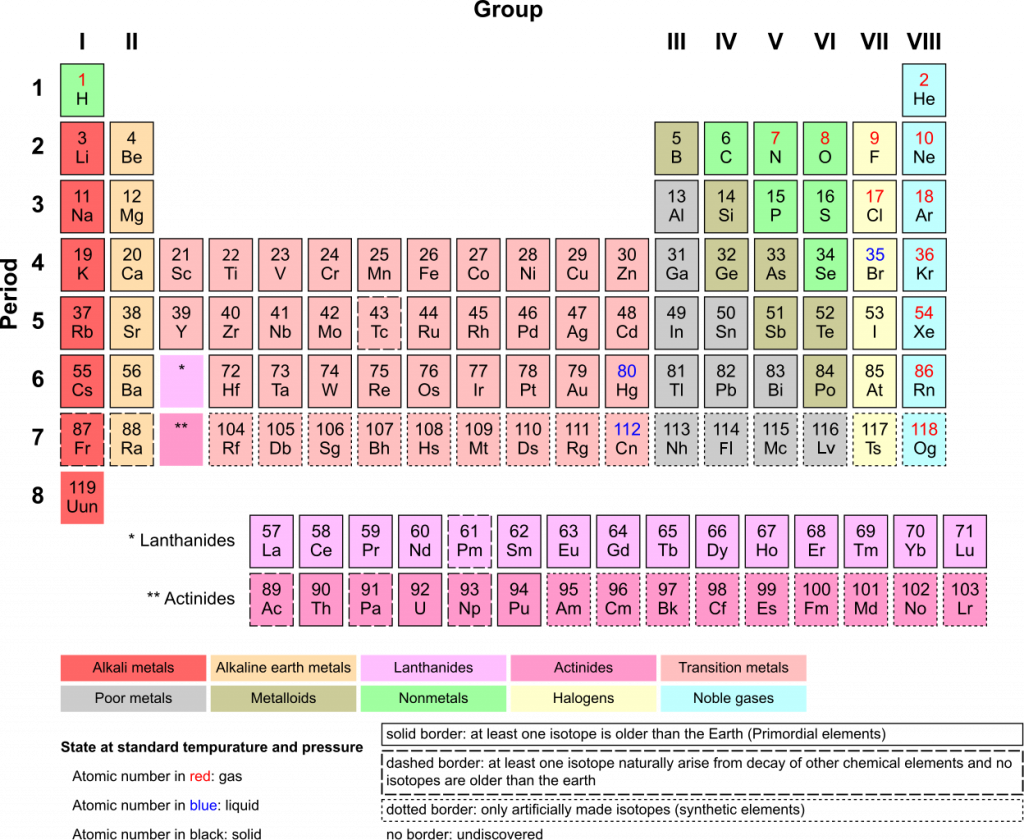
Quantum theory also explains ionization energy. A higher n value indicates a greater distance from the nucleus. The farther an electron is from the nucleus, the smaller the attraction between them. The lower the attraction, the easier it is to remove that electron. Since ionization energy is the energy required to remove an electron, it decreases (ionization is easier) as n increases.
The valence (last or furthest from the nucleus) shell of any atom cannot have more than eight electrons. This is the most stable electron configuration. If an atom has one electron in its valence shell, it will require less energy to remove that one electron than to gain seven electrons to get to a full electron configuration. This means that it will have a low ionization energy and a low electron affinity. As an atom approaches eight valence electrons, its ionization energy increases. Electrons with full valence shells (noble gases) have incredibly high ionization energies because they already have a full valence shell.
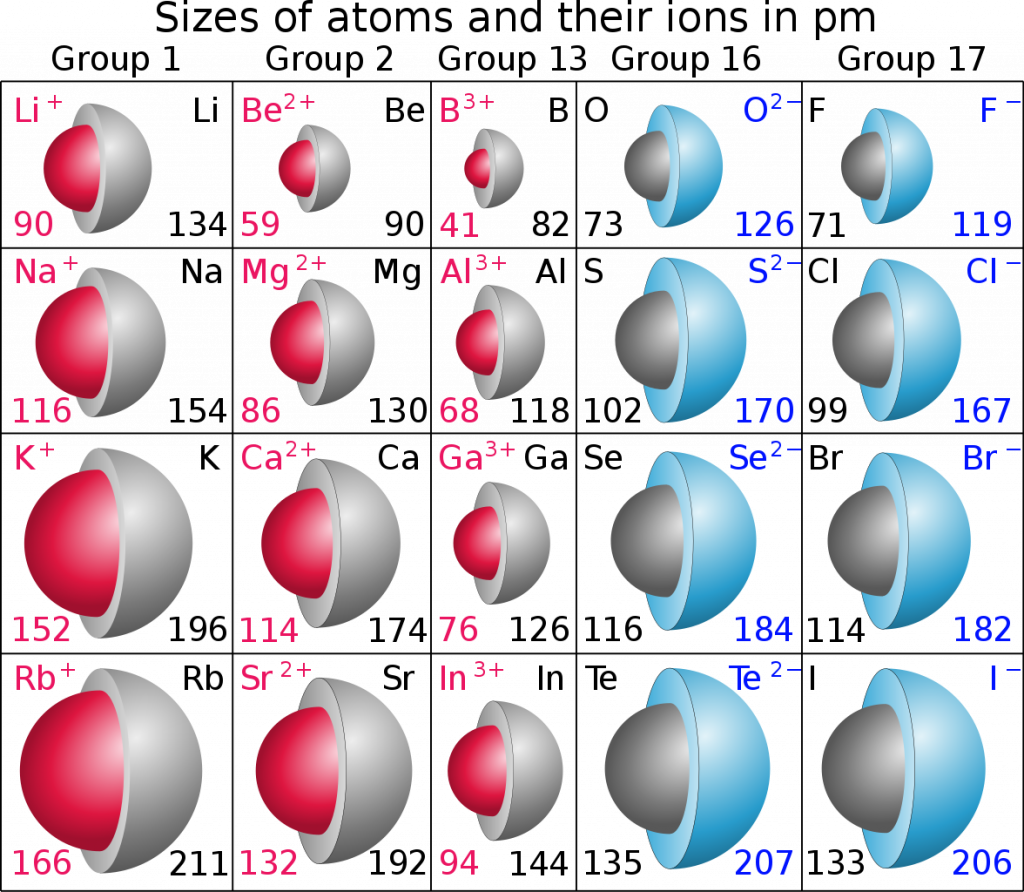
As you move across the periodic table from left to right, ionization energy increases because valence electrons increase. This tendency is called a periodic trend. Ionization energy decreases as you move down the periodic table. This is because as you move down the periodic table, the size of the atoms increases. As size increases, the valence electrons are further and further from the nucleus, decreasing their electron affinity and therefore decreasing their ionization energy.
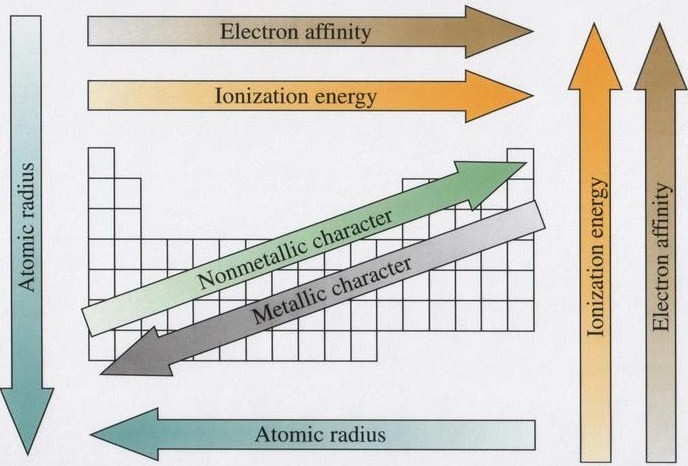
So even though the electrons in barium are in a higher energy level than beryllium, they are further away from the nucleus, meaning they have less affinity for the nucleus. This makes removing an electron take less energy, so barium has a lower ionization energy than beryllium. By the same logic, barium has a lower ionization energy than mercury because barium has fewer electrons in its valence shell.
Examples:
1. To determine which of two electrons has a higher ionization energy, look at their n values. A higher n means a higher ionization energy. If the n values are the same, then the electron with the higher l or m_l value.
2. When determining which element has a higher ionization energy, compare their locations on the periodic table. Remember, that ionization energy increases as you go up and to the right on the periodic table. This means that fluorine has a higher ionization energy than lithium, cadmium is higher than barium, chlorine is higher than gold, and silicon is higher than lead.
Key Concept: Ionization energy tends to increase as you move up and right on the periodic table. This is the same trend as atomic size and electron affinity and the opposite trend as atomic radius.
Atomic Radius Trend
Conclusion and Summary
We’ve covered a lot in this AP® Chemistry Crash Course, so let’s take a moment to review:
• Each electron can be uniquely identified with four quantum numbers.
• The principal quantum number, n, describes the distance from the nucleus. This quantum number can be any whole number greater than or equal to 1.
• The angular momentum quantum number, l, describes the shape of the electron’s orbital. The angular momentum quantum number can have a value ranging from 0 to n-1. Angular momentum quantum numbers are also labeled with letters.
‣ l=0 are s orbitals
‣ l= 1 are p orbitals
‣ l = 2 are d orbitals
‣ l = 3 are f orbitals
• The magnetic quantum number, m_l, describes the orientation of the orbital. This number can be any integer between -l and +l.
• The spin quantum number, m_s, describes the spin of the electron. This number is either +\dfrac{1}{2} (spin up) or -\dfrac{1}{2} (spin down).
• The quantum numbers of electrons can be related to the properties of atoms such as ionization energy and the absorption of light.
This covers just about everything you’ll need to know about quantum numbers and theory for the AP® Chemistry exam. You are guaranteed to see some of this topic on your exam, so be sure to reread this article as much as you need to get up to speed on everything quantum for AP® Chemistry.
Looking for AP® Chemistry practice?
Check out our other articles on AP® Chemistry.
You can also find thousands of practice questions on Albert.io. Albert.io lets you customize your learning experience to target practice where you need the most help. We’ll give you challenging practice questions to help you achieve mastery of AP® Chemistry.
Start practicing here.
Are you a teacher or administrator interested in boosting AP® Chemistry student outcomes?
Learn more about our school licenses here.








