Introduction

Linear regression models find several uses in real-life problems. For example, a multi-national corporation wanting to identify factors that can affect the sales of its product can run a linear regression to find out which factors are important. In econometrics, Ordinary Least Squares (OLS) method is widely used to estimate the parameter of a linear regression model. OLS estimators minimize the sum of the squared errors (a difference between observed values and predicted values). While OLS is computationally feasible and can be easily used while doing any econometrics test, it is important to know the underlying assumptions of OLS regression. This is because a lack of knowledge of OLS assumptions would result in its misuse and give incorrect results for the econometrics test completed. The importance of OLS assumptions cannot be overemphasized. The next section describes the assumptions of OLS regression.

Assumptions of OLS Regression

The necessary OLS assumptions, which are used to derive the OLS estimators in linear regression models, are discussed below.

OLS Assumption 1: The linear regression model is “linear in parameters.”

When the dependent variable (Y) is a linear function of independent variables (X's) and the error term, the regression is linear in parameters and not necessarily linear in X's. For example, consider the following:

A1. The linear regression model is “linear in parameters.”

A2. There is a random sampling of observations.

A3. The conditional mean should be zero.

A4. There is no multi-collinearity (or perfect collinearity).

A5. Spherical errors: There is homoscedasticity and no autocorrelation

A6: Optional Assumption: Error terms should be normally distributed.

a)\quad Y={ \beta }_{ 0 }+{ \beta }_{ 1 }{ X }_{ 1 }+{ \beta }_{ 2 }{ X }_{ 2 }+\varepsilon

b)\quad Y={ \beta }_{ 0 }+{ \beta }_{ 1 }{ X }_{ { 1 }^{ 2 } }+{ \beta }_{ 2 }{ X }_{ 2 }+\varepsilon

c)\quad Y={ \beta }_{ 0 }+{ \beta }_{ { 1 }^{ 2 } }{ X }_{ 1 }+{ \beta }_{ 2 }{ X }_{ 2 }+\varepsilon

In the above three examples, for a) and b) OLS assumption 1 is satisfied. For c) OLS assumption 1 is not satisfied because it is not linear in parameter { \beta }_{ 1 }.

OLS Assumption 2: There is a random sampling of observations

This assumption of OLS regression says that:

• The sample taken for the linear regression model must be drawn randomly from the population. For example, if you have to run a regression model to study the factors that impact the scores of students in the final exam, then you must select students randomly from the university during your data collection process, rather than adopting a convenient sampling procedure.
• The number of observations taken in the sample for making the linear regression model should be greater than the number of parameters to be estimated. This makes sense mathematically too. If a number of parameters to be estimated (unknowns) are more than the number of observations, then estimation is not possible. If a number of parameters to be estimated (unknowns) equal the number of observations, then OLS is not required. You can simply use algebra.
• The X's should be fixed (e. independent variables should impact dependent variables). It should not be the case that dependent variables impact independent variables. This is because, in regression models, the causal relationship is studied and there is not a correlation between the two variables. For example, if you run the regression with inflation as your dependent variable and unemployment as the independent variable, the OLS estimators are likely to be incorrect because with inflation and unemployment, we expect correlation rather than a causal relationship.
• The error terms are random. This makes the dependent variable random.

OLS Assumption 3: The conditional mean should be zero.

The expected value of the mean of the error terms of OLS regression should be zero given the values of independent variables.

Mathematically, E\left( { \varepsilon }|{ X } \right) =0. This is sometimes just written as E\left( { \varepsilon } \right) =0.

In other words, the distribution of error terms has zero mean and doesn’t depend on the independent variables X's. Thus, there must be no relationship between the X's and the error term.

OLS Assumption 4: There is no multi-collinearity (or perfect collinearity).

In a simple linear regression model, there is only one independent variable and hence, by default, this assumption will hold true. However, in the case of multiple linear regression models, there are more than one independent variable. The OLS assumption of no multi-collinearity says that there should be no linear relationship between the independent variables. For example, suppose you spend your 24 hours in a day on three things – sleeping, studying, or playing. Now, if you run a regression with dependent variable as exam score/performance and independent variables as time spent sleeping, time spent studying, and time spent playing, then this assumption will not hold.

This is because there is perfect collinearity between the three independent variables.

Time spent sleeping = 24 – Time spent studying – Time spent playing.

In such a situation, it is better to drop one of the three independent variables from the linear regression model. If the relationship (correlation) between independent variables is strong (but not exactly perfect), it still causes problems in OLS estimators. Hence, this OLS assumption says that you should select independent variables that are not correlated with each other.

An important implication of this assumption of OLS regression is that there should be sufficient variation in the X's. More the variability in X's, better are the OLS estimates in determining the impact of X's on Y.

OLS Assumption 5: Spherical errors: There is homoscedasticity and no autocorrelation.

According to this OLS assumption, the error terms in the regression should all have the same variance.

Mathematically, Var\left( { \varepsilon }|{ X } \right) ={ \sigma }^{ 2 }.

If this variance is not constant (i.e. dependent on X’s), then the linear regression model has heteroscedastic errors and likely to give incorrect estimates.

This OLS assumption of no autocorrelation says that the error terms of different observations should not be correlated with each other.

Mathematically, Cov\left( { { \varepsilon }_{ i }{ \varepsilon }_{ j } }|{ X } \right) =0\enspace for\enspace i\neq j

For example, when we have time series data (e.g. yearly data of unemployment), then the regression is likely to suffer from autocorrelation because unemployment next year will certainly be dependent on unemployment this year. Hence, error terms in different observations will surely be correlated with each other.

In simple terms, this OLS assumption means that the error terms should be IID (Independent and Identically Distributed).

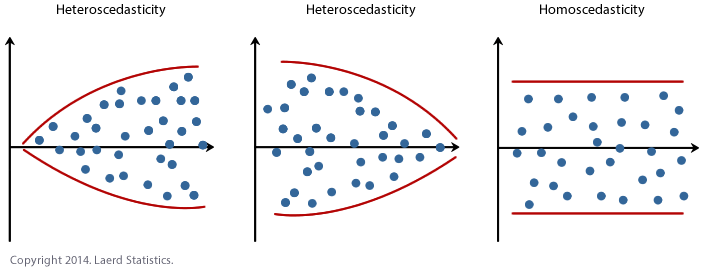
The above diagram shows the difference between Homoscedasticity and Heteroscedasticity. The variance of errors is constant in case of homoscedasticity while it’s not the case if errors are heteroscedastic.

OLS Assumption 6: Error terms should be normally distributed.

This assumption states that the errors are normally distributed, conditional upon the independent variables. This OLS assumption is not required for the validity of OLS method; however, it becomes important when one needs to define some additional finite-sample properties. Note that only the error terms need to be normally distributed. The dependent variable Y need not be normally distributed.

The Use of OLS Assumptions

OLS assumptions are extremely important. If the OLS assumptions 1 to 5 hold, then according to Gauss-Markov Theorem, OLS estimator is Best Linear Unbiased Estimator (BLUE). These are desirable properties of OLS estimators and require separate discussion in detail. However, below the focus is on the importance of OLS assumptions by discussing what happens when they fail and how can you look out for potential errors when assumptions are not outlined.

1. The Assumption of Linearity (OLS Assumption 1) – If you fit a linear model to a data that is non-linearly related, the model will be incorrect and hence unreliable. When you use the model for extrapolation, you are likely to get erroneous results. Hence, you should always plot a graph of observed predicted values. If this graph is symmetrically distributed along the 45-degree line, then you can be sure that the linearity assumption holds. If linearity assumptions don’t hold, then you need to change the functional form of the regression, which can be done by taking non-linear transformations of independent variables (i.e. you can take log { X } instead of X as your independent variable) and then check for linearity.
2. The Assumption of Homoscedasticity (OLS Assumption 5) – If errors are heteroscedastic (i.e. OLS assumption is violated), then it will be difficult to trust the standard errors of the OLS estimates. Hence, the confidence intervals will be either too narrow or too wide. Also, violation of this assumption has a tendency to give too much weight on some portion (subsection) of the data. Hence, it is important to fix this if error variances are not constant. You can easily check if error variances are constant or not. Examine the plot of residuals predicted values or residuals vs. time (for time series models). Typically, if the data set is large, then errors are more or less homoscedastic. If your data set is small, check for this assumption.
3. The Assumption of Independence/No Autocorrelation (OLS Assumption 5) – As discussed previously, this assumption is most likely to be violated in time series regression models and, hence, intuition says that there is no need to investigate it. However, you can still check for autocorrelation by viewing the residual time series plot. If autocorrelation is present in the model, you can try taking lags of independent variables to correct for the trend component. If you do not correct for autocorrelation, then OLS estimates won’t be BLUE, and they won’t be reliable enough.
4. The Assumption of Normality of Errors (OLS Assumption 6) – If error terms are not normal, then the standard errors of OLS estimates won’t be reliable, which means the confidence intervals would be too wide or narrow. Also, OLS estimators won’t have the desirable BLUE property. A normal probability plot or a normal quantile plot can be used to check if the error terms are normally distributed or not. A bow-shaped deviated pattern in these plots reveals that the errors are not normally distributed. Sometimes errors are not normal because the linearity assumption is not holding. So, it is worthwhile to check for linearity assumption again if this assumption fails.
5. Assumption of No Multicollinearity (OLS assumption 4) – You can check for multicollinearity by making a correlation matrix (though there are other complex ways of checking them like Variance Inflation Factor, etc.). Almost a sure indication of the presence of multi-collinearity is when you get opposite (unexpected) signs for your regression coefficients (e. if you expect that the independent variable positively impacts your dependent variable but you get a negative sign of the coefficient from the regression model). It is highly likely that the regression suffers from multi-collinearity. If the variable is not that important intuitively, then dropping that variable or any of the correlated variables can fix the problem.
6. OLS assumptions 1, 2, and 4 are necessary for the setup of the OLS problem and its derivation. Random sampling, observations being greater than the number of parameters, and regression being linear in parameters are all part of the setup of OLS regression. The assumption of no perfect collinearity allows one to solve for first order conditions in the derivation of OLS estimates.

Conclusion

Linear regression models are extremely useful and have a wide range of applications. When you use them, be careful that all the assumptions of OLS regression are satisfied while doing an econometrics test so that your efforts don’t go wasted. These assumptions are extremely important, and one cannot just neglect them. Having said that, many times these OLS assumptions will be violated. However, that should not stop you from conducting your econometric test. Rather, when the assumption is violated, applying the correct fixes and then running the linear regression model should be the way out for a reliable econometric test.

Do you believe you can reliably run an OLS regression? Let us know in the comment section below!

Looking for Econometrics practice?

You can find thousands of practice questions on Albert.io. Albert.io lets you customize your learning experience to target practice where you need the most help. We’ll give you challenging practice questions to help you achieve mastery of Econometrics.

Start practicing here.

Are you a teacher or administrator interested in boosting AP® Biology student outcomes?

Learn more about our school licenses here.