Just like the English language can be translated into other languages, we can also translate it into the language of math. Many words we use every day can imply different mathematical operations. For example, “total” might indicate the equal sign, and “increase by” could mean the addition symbol. Being able to translate from English into math allows us to turn words into equations. Keep reading to see how this works for writing systems of equations.

What is a System of Equations?

Before we start writing systems of equations, let’s make sure we know what a system of equations is. A system of equations is simply two or more equations that share the same variables. In Algebra 1, you will mainly focus on systems with two equations and two variables.

The two variables you likely know best are x and y. You may be wondering, why x and y? The axes of a coordinate plane are the x-axis and y-axis. So, the x and y in the equations represent the x and y coordinates on a graph. When you solve a system of equations with two variables, it is your goal to find the point — (x,y) — where the two graphs intersect. This point of intersection is the solution to the system of equations.

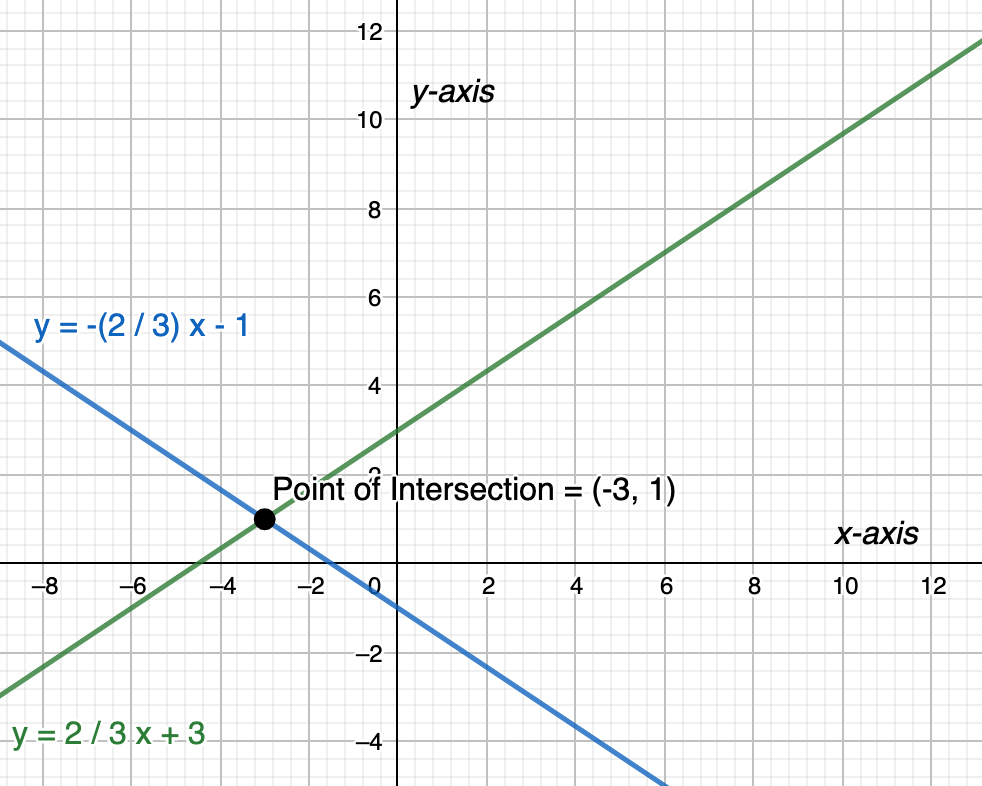
You might also notice that most systems of equations you solve in Algebra 1 are systems of two linear equations. To review linear equations and their many different forms, check out the Albert blog post Forms of Linear Equations.

Looking ahead: What if you have three equations and three variables, making a three-variable system of equations? You will need a third axis, the z-axis.

Examples of Systems of Equations

Did you know that there are multiple ways to represent a system of equations? The four main ways you will see a system of equations represented are by its equations (algebra), a table (numbers), a graph (visual), and a verbal description (words). Let’s take a look at what each form looks like using a system of two linear equations:

Equation (algebra) form:

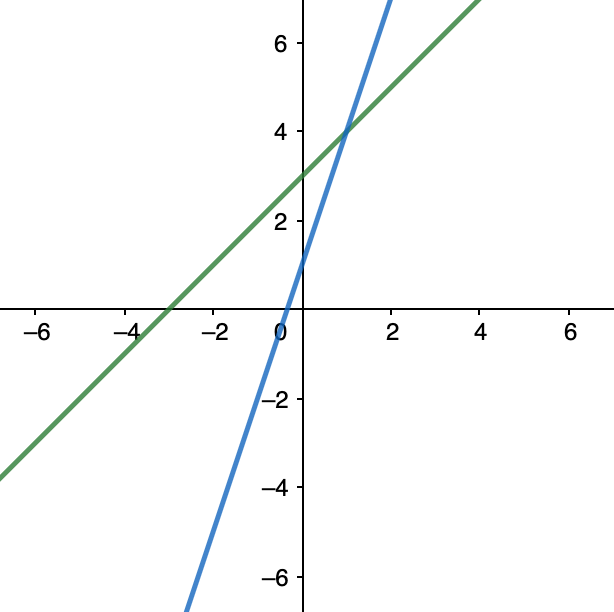
y=3x+1 

y=x+3

Table (numbers) form:

x_1	-2	-1	0	1	2
y_1	-5	-2	1	4	7
y_2	1	2	3	4	5

Graph (visual) form:

Verbal Description (words) form:

You and a friend are in a reading club. Before the club starts, you have read 1 book, and your friend has read  3  books. You set a goal to read  3 books every month, and your friend sets a goal to read 1  book every month. From this description, you could write a system of equations and solve to answer the question: After how many months will you and your friend have read the same number of books?

Now that we have explored the different ways to represent a system of linear equations, we will see how to write a system of linear equations. The following sections of this post will investigate how to write the equation form of a system of equations from a table, a graph, and a verbal description or what your teacher probably calls word problems.

How to Write a System of Equations

Writing Systems of Equations from a Table

Writing a system of linear equations from a table is just like writing a linear equation from a table. However, this time we will be writing two equations. Let’s remember the two things you need to calculate from the table to write a linear equation: 1) the slope and 2) the y-intercept. If you are lucky, the y-intercept will be in the table. If not, then there is a little more work to do, but you can still do it!

Let’s look at the table below to practice writing a system of linear equations from a table:

x	-5	-2	1	4
y_1	-2	0	2	4
y_2	-2	-5	-8	-11

Notice there is only one x row while there are two y rows because our table is showing a system of TWO equations. We can separate this table into two tables, one for each equation:

x	-5	-2	1	4
y_1	-2	0	2	4

x	-5	-2	1	4
y_2	-2	-5	-8	-11

Now we need to apply our writing linear equation skills and calculate the slope and the y-intercept from each table. Remember, the slope-intercept form of an equation is y=mx +b , where m represents the slope and b represents the y-intercept.

You can find the slope of the first table by calculating the ratio of the change in y values to the change in x values using two points from the table, such as (-2, 0) and (1, 2):

m=\dfrac{y_2-y_1}{x_2-x_1}

m=\dfrac{2-0}{1-(-2)}

m=\dfrac{2}{3}

Now, we need to use a point in the table to calculate the y-intercept. Let’s use the point ( -2, 0). Substitute -2 for x, 0 for y, and \frac{2}{3} for m in the equation and solve for b.

y=\dfrac{2}{3} x +b

0=\dfrac{2}{3}( -2) +b

0=-\dfrac{4}{3}+b

\dfrac{4}{3}=b

Now that we know the slope and y-intercept, we can write our first equation: 

y_1=\dfrac{2}{3}x+\dfrac{4}{3}

We can use this same process to write the second equation in our system. First, calculate the slope as the ratio of the change in y values to the change in x values between two points, such as (1, -8) and (4, -11):

m=\dfrac{y_2-y_1}{x_2-x_1}

m=\dfrac{-11-(-8)}{4-1}

m=\dfrac{-3}{3}

m=-1

And once more, we can calculate the y-intercept by substituting a point — such as (1, -8) – into our equation and solving for b.

y=- x +b

-8=- (1) +b

-8=-1+b

-7=b

So, our second equation is y_2= -x-7. We can now write our system of equations for the given table:

y_1=\dfrac{2}{3}x+\dfrac{4}{3}

y_2=-x-7

If you are having trouble writing linear equations using a table or two points, then check out these Albert blogs to help: How to Find Slope and Slope-Intercept Form.

Writing Systems of Equations from a Graph

Writing a system of linear equations from a graph is like writing a system from a table. We need to identify the slope and the y-intercept of each line in the graph to write our system of equations.

Let’s look at the graph given below to practice writing a system of linear equations from a graph:

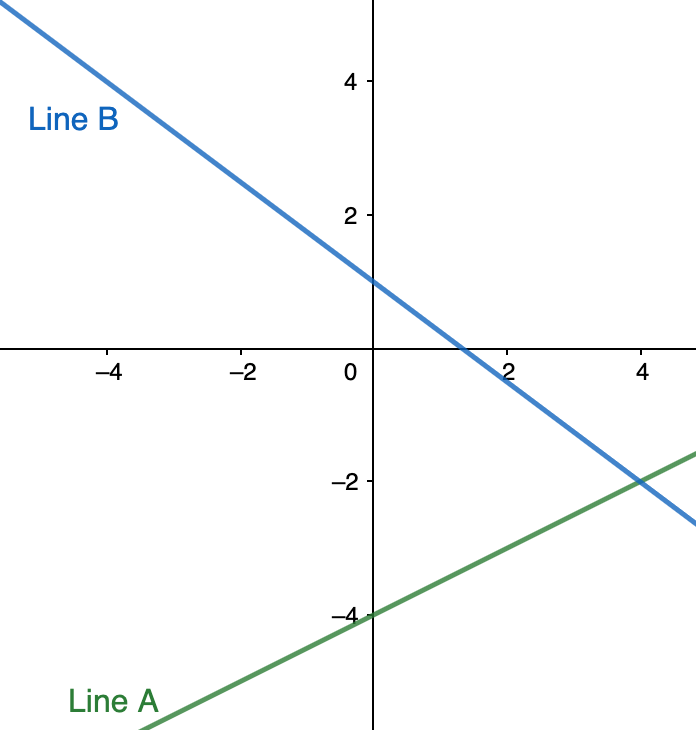
Starting with line A, let’s calculate the slope. We can use the slope formula and the points (0, -4) and (4, -2) to find the slope:

m=\dfrac{y_2-y_1}{x_2-x_1}

m=\dfrac{-2-(-4)}{4-0}

m=\dfrac{2}{4}

m=\dfrac{1}{2}

Let’s repeat this process with two points from line B, such as (0, 1) and (4, -2):

m=\dfrac{-2-1}{4-0}

m=\dfrac{-3}{4}

m=-\dfrac{3}{4}

Next, we can identify the y-intercepts of each line from the graph. Remember, the y-intercept is always where the line crosses the y-axis and where the {x} coordinate is {0}:

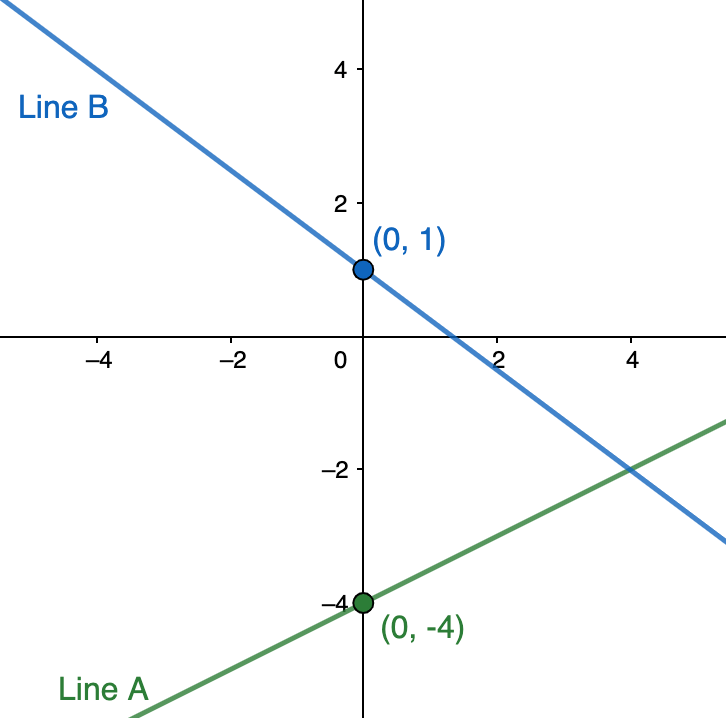
So, the y-intercept of line A is -4 and the y-intercept of line B is 1. Now we can substitute the slopes and y-intercepts of our two lines into equations in the form y=mx+b to create our system:

y=\dfrac{1}{2}x - 4

y=-\dfrac{3}{4}x+1

If you are having trouble writing linear equations using a graph or two points, then check out these Albert blogs to help: How to Find Slope and Slope-Intercept Form.

Writing Systems of Equations from Word Problems

When writing systems of equations from word problems, it is important to create a list of common translations from words to their equivalent math operations. If you haven’t done this in class yet, here is a table to get you started:

Math Operation	Words/Phrases
=	equals, total, is, final
+	add, sum, combine, and, greater than
-	subtract, difference, minus, less than
\times	multiply, times, double, by
\div	divide, ratio, split, half, share

To practice writing systems of equations from word problems, let’s take a look at the following two examples:

Example 1: At the end of a basketball game, your team’s final score was 53 points. You know that the team scored 23 baskets altogether. Some baskets were worth 2 points, and others were worth 3 points. Surprisingly, no one made it to the free-throw line. Write a system of equations to represent this situation.

Step 1: Write down what you know from the problem.

• the team scored 53 points
• a total of 23 baskets were scored

Step 2: Write down all the unknowns of the situation.

• number of 2-point baskets 
• number of 3-point baskets

Step 3: Define your variables.

This is a crucial step that can feel overwhelming. However, if you have identified the words in the word problem that tell you what is unknown, you now have your variable definitions. Remember, a variable represents an unknown.

• x: number of 2-point baskets
• y: number of 3-point baskets

Step 4: Write mathematical sentences using your variables (unknowns) and the given information. 

Notice that the important information identified represents totals or a final score. These values will go after the equal sign. You need to figure out how your variables (unknowns) relate to the final score and the total number of baskets. Let’s take a look:

• The number of 2-point baskets and the number of 3-point baskets is a total of 23 baskets scored.
• 2 times the number of 2-point baskets and 3 times the number of 3-point baskets equals a final score of 53 points.

Step 5: Translate your math sentences into equations.

Remember to use the table above and look for words that can translate to a math operation.

• x+y= 23
• 2x + 3y = 53

Step 6: Write your system of equations for the word problem.

 x + y = 23

2x + 3y = 53

Example 2: Two numbers have a difference of 7, and when combined, their sum is 33. Write a system of equations to represent this situation.

Step 1: Write down what you know from the problem.

• two numbers have a difference of 7
• the same two numbers combine to a sum of 33

Step 2: Write down all the unknowns of the situation.

Since the two numbers have a difference, one number must be larger, and one number must be smaller.

• the value of the smaller number
• the value of the greater number

Step 3: Define your variables.

• x: smaller number
• y: larger number

Step 4: Write mathematical sentences using your variables (unknowns) and the given information. 

Notice there are multiple words in the original problem that can be translated to math operations: the word difference means to subtract (minus) and the words sum and combine mean to add. Let’s take a look:

• Larger number minus the smaller number is a difference of 7.
• Larger number combined with the smaller number is a sum of 33.

Step 5: Translate your math sentences into equations.

• y - x = 7
• y + x = 33

Step 6: Write your system of equations for the word problem.

y – x = 7

y + x = 33

For more practice writing systems of equations from word problems, check out this video example.

Writing Systems of Equations: Keys to Remember

• A system of equations is when you have two or more equations that share the same variables.
• Four ways to represent a system of equations are by its equations (algebra), a table (numbers), a graph (visual), and a verbal description (words). 
• To write a system of linear equations from a table or graph, you must calculate the slope and the y-intercept.
• To write a system of linear equations from a word problem, you need to translate the words into math sentences to create equations.