Wave interference plays a critical role in shaping the behaviors and characteristics of waves in various media. In this blog post, we’ll break down wave interference, focusing on constructive and destructive interference. We’ll also review the principle of superposition and apply it to some examples. Through engaging examples and clear explanations, we aim to offer a comprehensive review of these fascinating phenomena. 

What is Wave interference?

Wave interference is the phenomenon that occurs when two or more waves interact with each other. The net effect of their interaction depends on their relative phases and amplitudes, giving rise to constructive or destructive interference.

Constructive Wave Interference

Constructive interference happens when waves are in phase with each other, meaning their peaks and troughs align. In this case, the resultant wave will have an amplitude that is the sum of the individual wave amplitudes. Imagine two water waves approaching each other with identical amplitudes and wavelengths. When they meet, their peaks will add up, creating a wave that’s essentially twice as tall as the original waves. This is constructive interference in action.

In the image below, the top waves have amplitudes of 3\text{ units} and 5\text{ units}. Since they are in phase, they would interfere constructively with an amplitude of 8\text{ units}, as shown in the bottom wave.

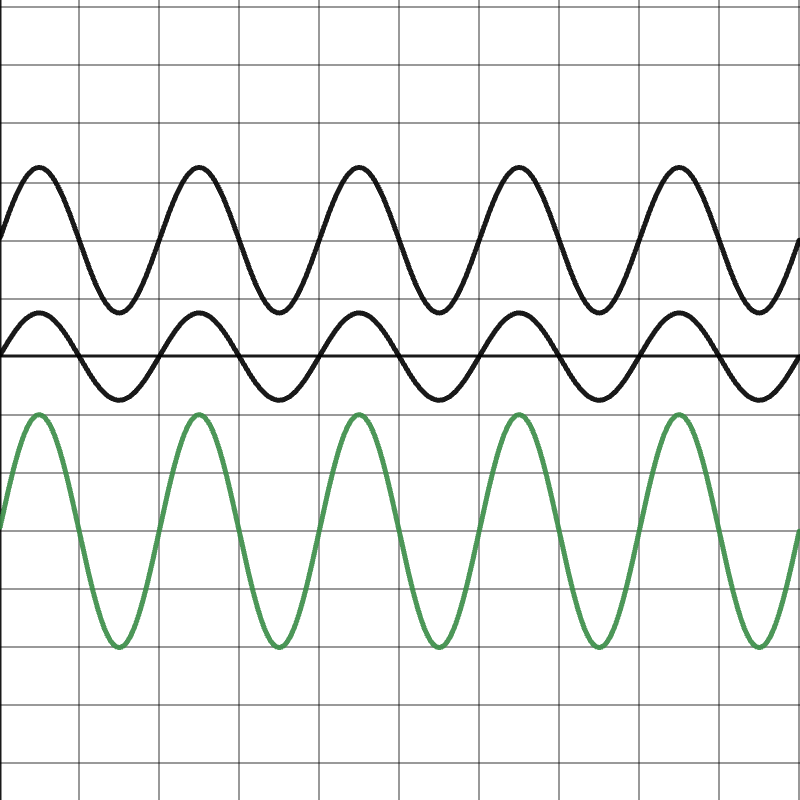
Destructive Wave Interference

Destructive interference occurs when waves are out of phase, i.e., when the peak of one wave coincides with the trough of another. When this happens, the waves cancel each other out, resulting in a reduced amplitude or, in some cases, complete cancellation. Consider noise-canceling headphones as a real-world example. These headphones produce sound waves that are out of phase with ambient noise. When these opposite waves meet, they cancel each other out, making your environment quieter. This is an instance of destructive interference.

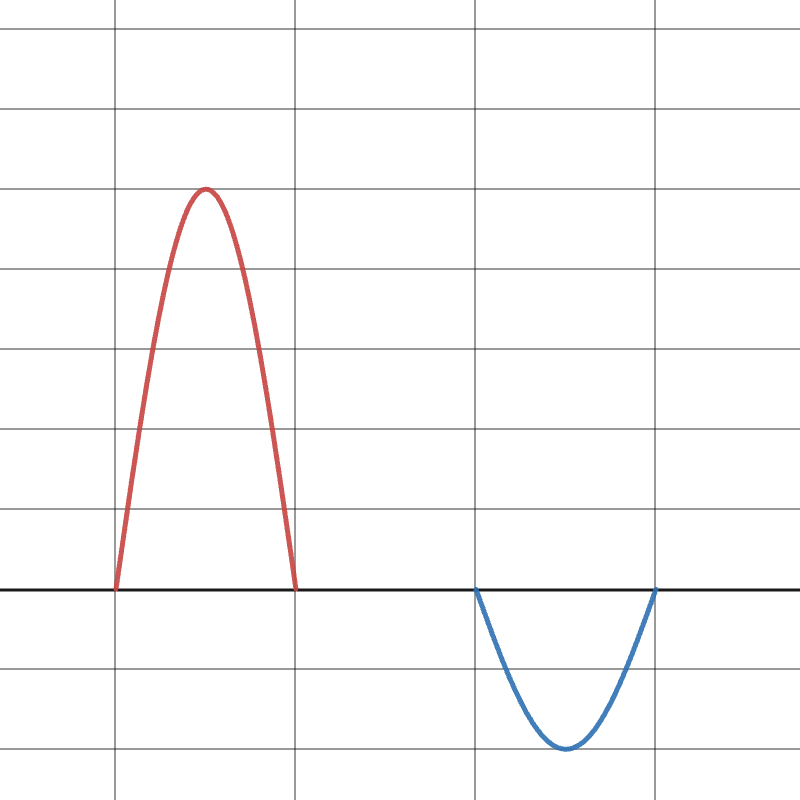
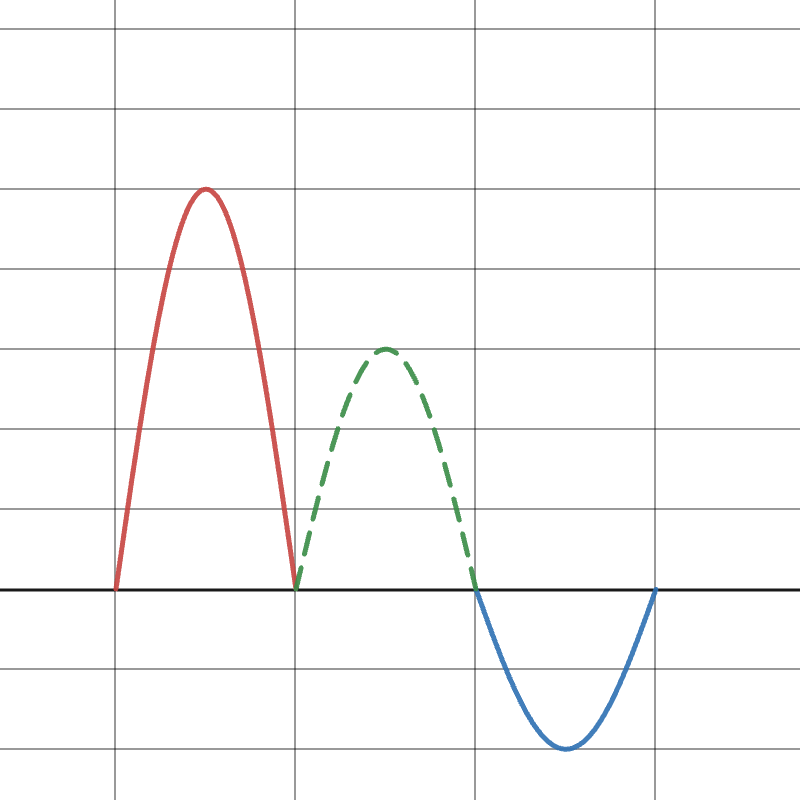
In the image below, the top waves have amplitudes of 8\text{ units} and 4\text{ units}. Since they are out of phase, they would experience destructive interference with an amplitude of 4\text{ units}, as shown in the bottom wave.

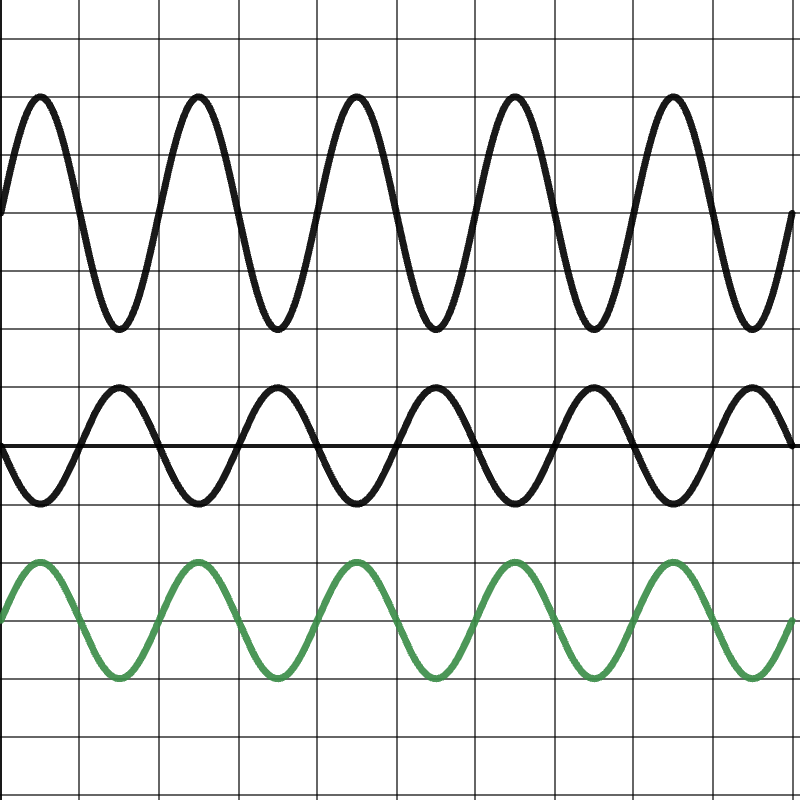
Wave interference isn’t limited to just one type of wave; it’s a phenomenon that can be observed across a variety of wave types. Let’s explore some of these.

What Kinds of Waves Can Show Interference?

Mechanical waves, like sound waves and water waves, can exhibit both constructive and destructive interference. For instance, when two speakers play the same frequency, you might notice areas where the sound is particularly loud (constructive interference) or unusually quiet (destructive interference).

Light waves, radio waves, and microwaves— all examples of electromagnetic waves—can also show interference patterns. The famous double-slit experiment, which demonstrates both constructive and destructive interference, can be performed with light.

Even seismic waves from earthquakes can undergo interference, affecting the distribution and intensity of the earthquake’s energy. This is crucial for understanding the potential impact of seismic activities.

Understanding the types of waves that can show interference broadens our grasp of this intriguing phenomenon and highlights its universal relevance in the study of physics.

The Principle of Superposition

The principle of superposition states that when two or more waves intersect, the resultant wave at any given point is the algebraic sum of the amplitudes of the individual waves. Simply put, if two waves meet at a point, you can find the resultant wave’s amplitude by either adding the amplitudes (for constructive interference) or subtracting them (for destructive interference).

Applying the Principle of Superposition

Before walking through some practice problems, let’s review the key principles. In constructive interference, the crest of one wave aligns with the crest of another, resulting in a larger amplitude wave. In destructive interference, the crest of one wave aligns with the trough of another, effectively canceling each other out or reducing the amplitude.

Practice and Examples

​​Practice Problem 1: Constructive Interference

Two sound waves are moving through the air. Wave A has an amplitude of 2\text{ units} and Wave B has an amplitude of 4\text{ units}. When they meet and undergo constructive interference, what is the amplitude of the resulting wave?

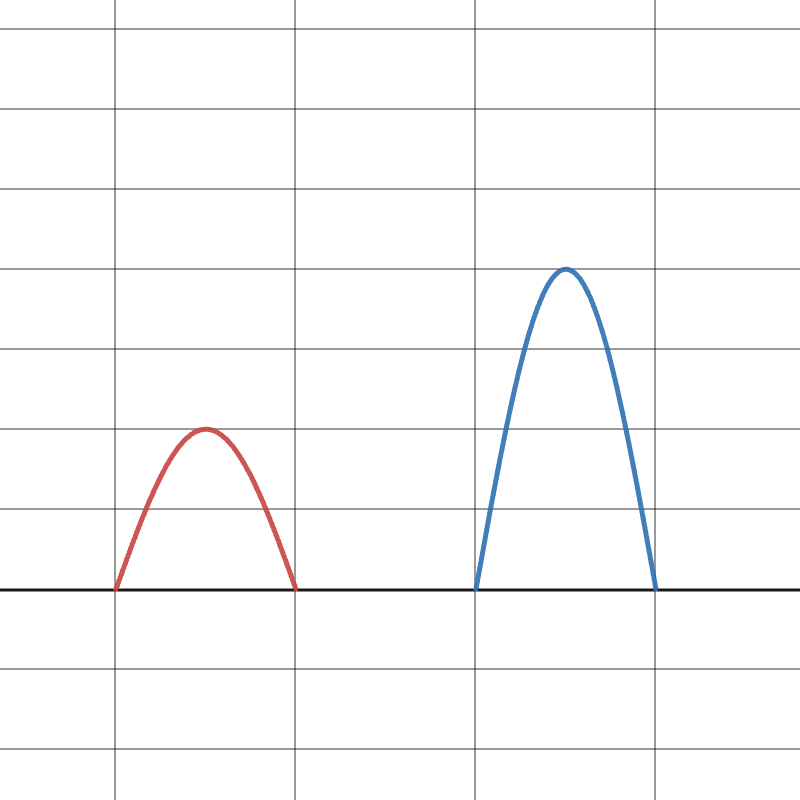
Step-by-Step Solution

In constructive interference, the amplitudes of the two waves add together. Let’s start by defining what we know:

• The amplitude of wave A: A_A = 2\text{ units}
• The amplitude of wave B: A_B = 4\text{ units}

Now we can add the two amplitudes together:

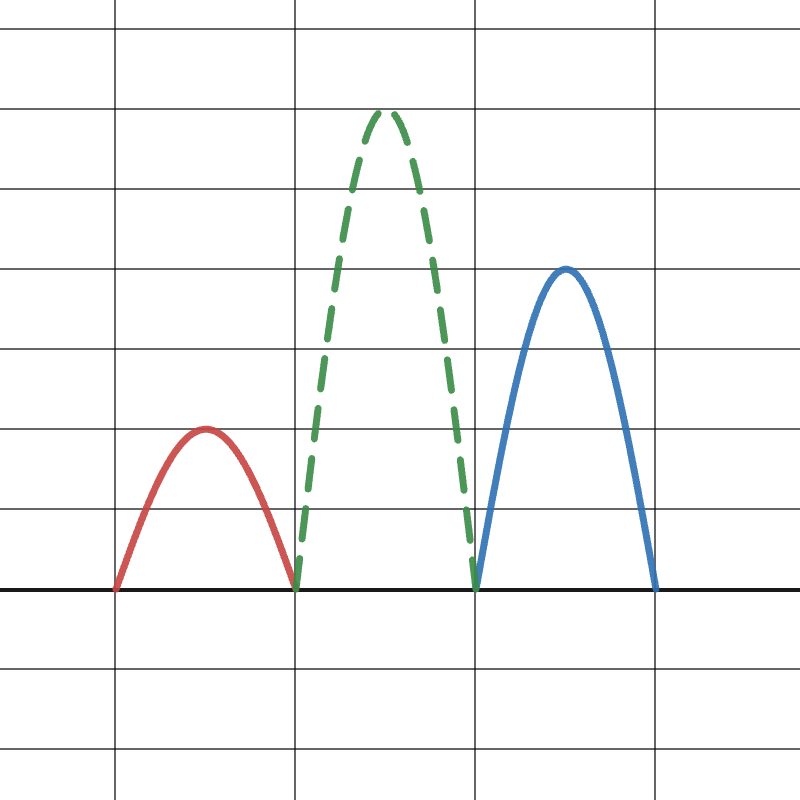
A_{result} = A_A + A_B = 2\text{ units} + 4\text{ units}

A_{result} = 6\text{ units}

The amplitude of the resulting wave is 6\text{ units}.

Practice Problem 2: Destructive Interference

Two water waves meet, with Wave X having an amplitude of 5\text{ cm} and Wave Y having an amplitude of 2\text{ cm}. What is the amplitude of the resulting wave after destructive interference?

Step-by-Step Solution

In destructive interference, the amplitudes subtract from each other. This is what we know:

• The amplitude of Wave X: A_X = 5\text{ cm}
• The amplitude of Wave Y: A_Y = 2\text{ cm}

Subtract the two amplitudes:

A_{result} =A_X -Z_Y = 5\text{ cm} - 2\text{ cm}

A_{result} = 3\text{ cm}

The amplitude of the resulting wave is 3\text{ cm}.

Strategies for Using the Principle of Superposition

If you’re trying to understand how waves combine or cancel each other out, the principle of superposition is your best friend. Here’s how you can use it like a pro:

1. Sketch the Waves: First, draw the individual waves on graph paper. This will help you visualize them better. You can use different colors for different waves to keep them separate in your mind.
2. Label What You Know: On your sketch, label the amplitudes, wavelengths, and any other known quantities. This will help you have all the information in one place.
3. Check for Phase: Are the waves in phase (peaks line up with peaks) or out of phase (peaks line up with troughs)? This will hugely impact how they combine.
4. Define Positive and Negative: Decide on a convention for what you will consider as “positive” and “negative” in terms of wave displacement. It may help to consider crests as positive amplitude and troughs as negative amplitude
5. Break It Down: Look at each individual wave and think about what it’s doing at the point where they meet. Write down or make a mental note of the amplitude of each wave at that point.
6. Add Them Up: Now add these amplitudes together, keeping in mind your positive and negative rules. This will give you the resulting wave’s amplitude at that point.

By taking it step-by-step and being thorough, you’ll find that complex wave interactions become much easier to understand and predict.

Conclusion

In this blog post, we reviewed many aspects of wave interference, covering essential concepts like constructive and destructive interference, as well as the principle of superposition. Through detailed explanations and step-by-step practice problems, we aimed to provide a comprehensive understanding of how waves interact when they meet. Whether you’re a high school student looking to ace your physics exam or someone curious about the science behind wave behaviors, we hope this guide has illuminated the intricacies of wave interference for you.