Ever wondered why the sound of an ambulance siren changes as it speeds past you? This captivating phenomenon is known as the Doppler effect. In this informative blog post, we’ll review what the Doppler effect is, explore the equation, and bring it to life with real-world examples.

The Doppler Effect

What is the Doppler Effect?

The Doppler effect is a fascinating physical phenomenon that occurs when the frequency of a wave changes based on the observer’s point of view. Think of it like this: when a sound-emitting object moves towards you, the waves get compressed, making the sound higher-pitched. Conversely, when the object moves away, the waves spread out, causing the pitch to drop. Essentially, the Doppler effect explains why a car engine or ambulance siren sounds different as it approaches, passes, and then moves away from you.

The Doppler Effect Equation

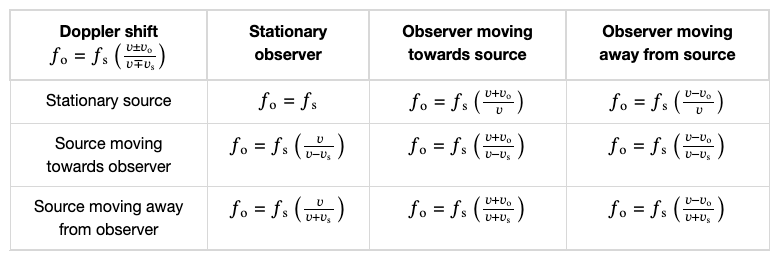
Now, let’s get a bit mathematical. The general Doppler effect equation can be used in a variety of settings, including moving and stationary sources and observers. The general equation is:

…where:

• $f_o$ is the frequency experienced by the observer
• $f_s$ is the frequency emitted by the source
• $v$ is the speed of the wave (most frequently the speed of sound or light)
• $v_o$ is the velocity of the observer ($0$ if it is at rest)
• $v_s$ is the velocity of the source ($0$ if it is at rest)

This equation allows us to calculate how much the frequency will change based on various speeds. Plus or minus is used depending on the direction of motion. The table below summarizes the variations of the formula for multiple settings:

The Doppler Effect in Sound

Sound is perhaps the most relatable example of the Doppler effect. When an ambulance approaches you, the siren sounds high-pitched. As it moves away, the siren lowers in pitch. In technical terms, this is because the sound waves are compressed as the ambulance approaches and stretched as it moves away, altering the frequency of the sound you hear.

The Doppler Effect in Light

But the Doppler effect isn’t limited to just sound; it also applies to light. You’ve likely heard of “redshift” and “blueshift” Doppler effect in the context of astronomy. When a star is moving away from Earth, its light appears more red due to the stretching of the light waves. On the other hand, if the star is moving towards Earth, its light appears more blue because the waves are compressed. This is a critical concept in astronomy for understanding the motion of celestial bodies.

Examples of the Doppler Effect

Problem-Solving Strategies

Solving problems using the Doppler effect equation uses a similar set of strategies for any Physics word problem.

• Sketch the Scenario: Always start by drawing a simple sketch. This will help you visualize who or what is moving: the source, the observer, or both.
• Identify What You Know: Label the known values like the speed of the source, the speed of the observer, and the original frequency.
• Choose the Right Equation: The Doppler effect equation changes slightly depending on the situation. Make sure to read the problem carefully to identify who is moving and in which direction, so you can select the appropriate Doppler effect equation for the situation.
• Plug in Values and Solve the Equation: Substitute the known values into the equation to solve for the unknown, which is often the observed frequency 
• Check Yourself: After solving the problem, see if your answer makes sense. For example, if the source and observer are moving toward each other, the observed frequency should be higher than the original. If they’re moving apart, it should be lower.

Let’s apply these strategies!

Moving Source

Let’s start by exploring a classic example of the Doppler effect where the source of the sound is moving. Imagine a police car with a siren emitting a frequency of $700\text{ Hz}$ is moving toward you at a speed of $30\text{ m/s}$. The speed of sound in air is approximately $343\text{ m/s}$. 

Steps to Solve the Problem

1. Identify Knowns and Unknowns

• Source frequency: $f_s = 700\text{ Hz}$
• Speed of sound: $v = 343\text{ m/s}$
• Speed of the police car (the source): $v_s = 30\text{ m/s}$
• Observed frequency: $f_o = ?$

2. Choose the Right Equation

Since only the source is moving, we’ll need an equation with a stationary observer:

$f_o = f_s \dfrac{{v}}{{v - v_{\text{{s}}}}}$

We subtract the speed of the source from the speed of sound because the source is getting closer to the observer.

3. Plug in Values

• $f_s = 100\text{ Hz}$
• $v = 343\text{ m/s}$
• $v_s = 30\text{ m/s}$

$f_o = f_s \dfrac{{v}}{{v - v_{\text{{s}}}}}$

$f_o = 700\text{ Hz} \cdot \dfrac{{343\text{ m/s}}}{{343\text{ m/s} - 30\text{ m/s}}}$

4. Solve the Equation

$f_o = 700\text{ Hz}\cdot \dfrac{{343\text{ m/s}}}{{313\text{ m/s}}} = 767\text{ Hz}$

5. Check Yourself

The frequency is higher than the source frequency ($700\text{ Hz}$), which makes sense because the source is moving toward the observer. The observed frequency is $767\text{ Hz}$.

Moving Observer

Now, consider an example of the Doppler effect where you are in a car moving away from a stationary siren emitting a frequency of $600\text{ Hz}$. Your car’s speed is $25\text{ m/s}$ and the speed of sound is $343\text{ m/s}$.

Steps to Solve the Problem

1. Identify Knowns and Unknowns

• Source frequency: $f_s = 600\text{ Hz}$
• Speed of sound: $v = 343\text{ m/s}$
• Your speed (the observer): $v_o = 25\text{ m/s}$
• Observed frequency: $f_o = ?$

2. Choose the Right Equation

Since only the observer is moving, we’ll need an equation with a stationary observer:

$f_o = f_s \dfrac{{v-v_o}}{{v }}$

We subtract the speed of the observer from the speed of sound because the source is getting farther from the observer.

3. Plug in Values

• $f_s = 600\text{ Hz}$
• $v = 343\text{ m/s}$
• $v_o = 25\text{ m/s}$

$f_o = f_s \dfrac{{v-v_o}}{{v }}$

$f_o = 600\text{ Hz} \cdot \dfrac{{343\text{ m/s}- 25\text{ m/s}}}{{343\text{ m/s}}}$

4. Solve the Equation

$f_o = 600\text{ Hz}\cdot \dfrac{{318\text{ m/s}}}{{343\text{ m/s}}} = 556\text{ Hz}$

5. Check Yourself

The frequency is lower than the source frequency ($600\text{ Hz}$), which makes sense because the observer is moving away from the source. The frequency heard is $556\text{ Hz}$.

Conclusion

In summary, we’ve reviewed the Doppler effect, exploring its fundamental principles, equations, and real-world applications in sound and light. Through a series of detailed examples, we’ve seen how this fascinating phenomenon affects our daily experiences, from the changing pitch of a passing ambulance siren to the shifting colors of celestial objects. We also offered problem-solving strategies to help you tackle these questions with confidence.