The center of mass (COM) is a fundamental concept in physics, especially in the realm of mechanics. It helps us understand how objects behave when forces are applied. Imagine it as the balancing point of an object, similar to how a seesaw needs to be perfectly balanced to not tip over. In this guide, the focus will be on defining what COM is, exploring the formula used to find it, examining various properties, and understanding its real-world applications.
What We Review
What is Center of Mass?
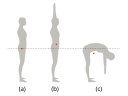
The center of mass of an object or system is the point where mass is evenly distributed in all directions. It acts as the average position of mass, meaning an object moves as if all its mass were concentrated at this single point. Understanding the center of mass is essential for analyzing stability, motion, and forces in physical systems.
For symmetrical objects with uniform density, the center of mass is at the geometric center. However, for irregularly shaped objects, it shifts toward the region with more mass. In dynamic systems, the it follows a predictable path, even if the object rotates or deforms.
Key Points
Motion Analysis: The center of mass determines how an object moves when subjected to forces. It helps explain the motion of everything from simple objects to complex systems like planets, vehicles, and the human body.
Balance Point: This point is where an object’s weight is evenly distributed. If supported here, the object remains stable without tipping.
The Formula
To find the center of mass, the formula used is:
\vec{x}_{cm} = \frac{\sum m_i \vec{x}_i}{\sum m_i}
Breaking Down the Formula:
- m_i: Mass of the individual object.
- \vec{x}_i: Position of each mass.
- \sum: Summation symbol, indicating that you add up all terms.
This formula calculates the exact point where the system balances.
Example 1: Finding the Center of Mass of Multiple Objects
Problem Statement: Calculate the center of mass for three objects with masses 2 kg, 4 kg, and 6 kg positioned at 1 m, 3 m, and 5 m on a straight line.
Solution Steps:
- Multiply each mass by its position:
- 2 \text{ kg} \cdot 1 \text{ m} = 2 \text{ kg}\cdot\text{m}
- 4 \text{ kg} \cdot 3 \text{ m} = 12 \text{ kg}\cdot\text{m}
- 6 \text{ kg} \cdot 5 \text{ m} = 30 \text{ kg}\cdot\text{m}
- Add these products: 2 + 12 + 30 = 44 \text{ kg}\cdot\text{m}
- Sum the masses: 2 \text{ kg} + 4 \text{ kg} + 6 \text{ kg} = 12 \text{ kg}
- Divide the total moment by the total mass: \vec{x}_{cm} = \frac{44 \text{ kg}\cdot\text{m}}{12 \text{ kg}} = 3.67 \text{ m}
Properties of the Center of Mass
It can behave in various ways depending on the system. In symmetrical objects, it is located at the geometric center.
Example 2: Symmetrical Object
Problem Statement: Determine the center of mass of a uniform rod of length 10 m.
Solution Steps:
- Recognize Uniform Distribution: The mass is evenly spread out.
- Locate Geometric Center: For a 10 m rod, the center is simply at 5 m.
No calculation is needed here because the object’s symmetry simplifies the problem.
The Role of External Forces and Interactions
The center of mass of a system can shift when an external force acts on it. However, forces that are internal to the system—such as interactions between objects within it—do not change the COM. This distinction is crucial in physics, especially in analyzing motion and stability.
When an external force acts on a system, the entire system’s center of mass moves accordingly. The new position is determined by averaging the positions of all mass components before and after the movement.
Effect of an External Force on the Center of Mass
- Initial Position: The center of mass starts at its original location.
- Applying Force: An external force causes a shift in the system’s mass distribution.
- Recalculation: The new COM is found by averaging the positions before and after the force was applied.
This principle applies in real-world scenarios, such as how a rocket’s center of mass shifts as it expels fuel or how an athlete’s center of mass changes during a jump.
Applications
The concept of center of mass is fundamental in various fields, including sports, engineering, and robotics, as it directly impacts stability, motion, and efficiency.
- Sports: Athletes adjust their COM to enhance balance, agility, and performance. In gymnastics, for example, controlling the center of mass helps in executing flips and landings. High jumpers use it strategically to clear the bar while keeping their actual body mass lower.
- Engineering: Structural stability relies on understanding the center of mass. Engineers design buildings, bridges, and vehicles with an optimized center of mass to prevent tipping and withstand external forces like wind and earthquakes.
- Robotics: Robots require precise control of their COM to maintain balance and movement efficiency. Humanoid robots, for instance, adjust their center of mass dynamically to walk, run, or handle uneven terrain without falling.
Conclusion
Understanding the center of mass provides insight into how objects balance and move. It’s a valuable tool not only in exams but for practical and innovative solutions in everyday applications.
| Term | Definition |
| Center of Mass | The point where the mass of a system is balanced in all directions. |
| Geometric Center | The central point of a symmetrical object. |
| External Forces | Forces acting on a system from the outside, affecting its center of mass. |
| Uniform Distribution | When mass is evenly spread throughout an object. |
Sharpen Your Skills for AP® Physics 1
Are you preparing for the AP® Physics 1 test? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world physics problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!
Need help preparing for your AP® Physics 1 exam?
Albert has hundreds of AP® Physics 1 practice questions, free response, and full-length practice tests to try out.








