In AP® Physics 1, understanding rotational motion equations is essential for analyzing how objects rotate around a fixed axis. Just as linear motion involves displacement, velocity, and acceleration, rotational motion has angular displacement, angular velocity, and angular acceleration governed by similar kinematic relationships. Mastering these equations helps solve problems involving torque, moment of inertia, and conservation of angular momentum, which appear frequently on the AP® exam and apply to real-world systems like gears, wheels, and pulleys.
What We Review
What is Rotational Motion?
Rotational motion occurs when an object spins around a central point or axis. Unlike linear motion, where objects move in a straight path, rotational motion involves spinning or circular movement. Understanding rotational motion is vital because it helps explain how everything from playground merry-go-rounds to complex machinery works.
Key Concepts
- Rotational Motion: Movement around an axis.
- Linear Motion: Movement along a straight path.
- Importance: It helps us understand circular movements in nature and technology.
Key Terms and Concepts in Rotational Motion
To dive deeper, familiarize oneself with terms like angular displacement, velocity, and acceleration. Angular displacement describes how far an object has rotated, measured in radians, while angular velocity and acceleration describe how quickly an object spins and its change in spinning speed, respectively.
Key Elements
- Radius r: Distance from the axis of rotation to a point in the body.
- Angle \theta: Rotational equivalent of distance in linear motion.
- Transitioning Concepts: Linear motion variables have rotational counterparts.
Rotational Motion Equations
Equations in rotational motion describe relationships mimicking those in linear motion but with rotational variables.
Important Formulas
- s = r\theta: Relates linear distance s and angular displacement \theta.
Example: Calculate the linear distance (s) a wheel of radius 0.5 meters covers when it rotates through 2 radians.
Solution:
- Identify known values: r = 0.5 \text{ meters}, \theta = 2 \text{ radians}.
- Use the formula s = r\theta.
- Substitute values: s = 0.5 \cdot 2 = 1 \text{ meter}.
Angular Velocity and Acceleration
Angular velocity \omega describes how fast an object rotates, equivalent to linear velocity in straight paths. While angular acceleration \alpha determines how quickly rotational speed changes.
Formulas:
- Linear velocity: v = r\omega
- Tangential acceleration: a_T = r\alpha
Example: Find the linear velocity (v) of a bike wheel with a radius of 0.3 meters and angular velocity of 4 radians/sec.
Solution:
- Known values: r = 0.3 \text{ meters}, \omega = 4 \text{ radians/sec}.
- Use v = r\omega.
- Substitute: v = 0.3 \cdot 4 = 1.2 \text{ m/s}.
The Relationship Between Linear and Rotational Motion
Translating linear to rotational concepts and vice versa helps in real-world applications. For example, in cars, the linear motion of the vehicle transitions into the angular motion of the wheels.
Example Problem
Calculate how a car’s linear motion affects the angular motion of its tires, given that the car travels at 20 m/s and the tire has a radius of 0.5 meters.
Solution:
- Linear speed: v = 20 \text{ m/s}.
- Tire radius: r = 0.5 \text{ meters}.
- Use formula v = r\omega \Rightarrow \omega = \frac{v}{r}.
- \omega = \frac{20}{0.5} = 40 \text{ radians/sec}.
Rigid Bodies in Rotational Motion
Rigid bodies do not change shape under rotational forces, maintaining a constant angular velocity unless influenced by external forces.
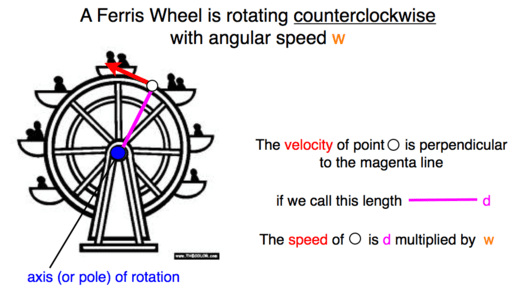
Example Problem
Determine the angular acceleration if a merry-go-round spins uniformly at 5 radians/sec and slows to stop in 10 seconds.
Solution:
- Initial velocity: \omega_i = 5 \text{ radians/sec}.
- Final velocity: \omega_f = 0 \text{ radians/sec}.
- Time: t = 10 \text{ sec}.
- Use \alpha = \frac{\omega_f - \omega_i}{t}.
- \alpha = \frac{0 - 5}{10} = -0.5 \text{ radians/sec}^2.
Summary: Connecting Rotational to Linear Motion
Navigating rotational motion concepts is essential for AP® Physics 1 and lays the foundation for deeper physics studies. Understanding these principles bridges theoretical knowledge with real-world applications, helping students analyze motion in spinning wheels, gears, and pulleys.
By mastering rotational motion equations and problem-solving strategies, you’ll be well-prepared for AP® Physics 1 exam questions and future applications in engineering and mechanics.
| Term | Definition |
| Angular Displacement | Angle over which an object rotates. |
| Angular Velocity | Rate of rotation, equivalent to rotational speed. |
| Radius r | Distance from axis of rotation. |
| Angular Acceleration | Rate of change of angular velocity over time. |
Sharpen Your Skills for AP® Physics 1
Are you preparing for the AP® Physics 1 test? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world physics problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!
Need help preparing for your AP® Physics 1 exam?
Albert has hundreds of AP® Physics 1 practice questions, free response, and full-length practice tests to try out.








