What We Review
Introduction
Conic sections are fascinating shapes that pop up all over math and science. These shapes come from slicing a double cone with a flat plane, and they each have unique properties of interest. Learning how to handle conic sections equations is a big deal for anyone studying AP® Precalculus. Why? Because these shapes model real-world phenomena like planetary orbits, satellite dishes, and the paths of projectiles. Now, let’s dive into the world of conic sections.
What Are Conic Sections?
Conic sections are curves obtained by intersecting a cone with a plane. The types of conic sections are:
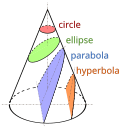
- Circle: A special type of ellipse where all points are equidistant from the center.
- Parabola: A U-shaped curve that can open up, down, left, or right.
- Ellipse: Looks like a stretched circle where the sum of distances from two points (foci) remains constant.
- Hyperbola: A pair of open curves that mirror each other, where the difference of distances from two points (foci) is constant.
Conic sections show up in nature and technology, like in the paths of comets or the design of optical lenses.
Conic Sections and Parabolas
A parabola is a neat shape found in things like satellite dishes and suspensions bridges due to its reflective property.
Standard Equations for Parabolas:
- Opens left/right: (y-k)^2 = a(x-h)
- Opens up/down: a(y-k) = (x-h)^2
Example Problem:
Find the equation of a parabola with vertex (2, -3) that opens upward and passes through the point (3, 0).
Solution Steps:
- Identify the vertex: h = 2, k = -3.
- Use the formula for a parabola opening upwards: a(y+3) = (x-2)^2.
- Substitute the given point to find a: a(0 + 3) = (3-2)^2.
- Solve for a: 3a = 1 \Rightarrow a = \frac{1}{3}.
- Write the final equation: \frac{1}{3}(y+3) = (x-2)^2.
Ellipses
An ellipse resembles a stretched circle and appears in planetary orbits and various engineering designs.
Standard Equation for Ellipses:
Centered at (h, k): \frac{(x-h)^2}{a^2} + \frac{(y-k)^2}{b^2} = 1
Example Problem:
Write the equation of an ellipse with a center at (4, 1), horizontal radius 3, and vertical radius 2.
Solution Steps:
- Identify values: h = 4, k = 1, a = 3, b = 2.
- Substitute into the formula: \frac{(x-4)^2}{3^2} + \frac{(y-1)^2}{2^2} = 1.
- Simplify the equation: \frac{(x-4)^2}{9} + \frac{(y-1)^2}{4} = 1.
Hyperbolas
Hyperbolas have two curves facing away from each other, with applications in navigation systems.
Standard Equations for Hyperbolas:
- Opens left/right: \frac{(x-h)^2}{a^2} - \frac{(y-k)^2}{b^2} = 1
- Opens up/down: -\frac{(x-h)^2}{a^2} + \frac{(y-k)^2}{b^2} = 1
Example Problem:
Find the equation of a hyperbola with center (0, 0), horizontal distance of 4, and vertical distance of 3.
Solution Steps:
- Identify values: h = 0, k = 0, a = 4, b = 3.
- Use left/right opening formula: \frac{x^2}{4^2} - \frac{y^2}{3^2} = 1.
- Simplify: \frac{x^2}{16} - \frac{y^2}{9} = 1.
Asymptotes of Hyperbolas
Asymptotes guide the hyperbola’s direction, never touching the curve but steering its path. They’re great for approximations.
Example Problem:
Determine the asymptotes for the hyperbola \frac{(x-1)^2}{25} - \frac{(y+2)^2}{16} = 1.
Solution Steps:
- Identify values: h = 1, k = -2, a^2 = 25, b^2 = 16.
- Use the formula for an asymptote equation in hyperbola: y = k \pm \frac{b}{a}(x-h).
- Substitute: y + 2 = \pm \frac{4}{5}(x - 1).
- Final equations: y = -2 \pm \frac{4}{5}(x - 1).
Quick Reference Chart
| Term | Definition |
| Conic Sections | Shapes formed by a plane cutting through a cone. |
| Parabola | A curve where distances from a point and line are equal. |
| Ellipse | A stretched circle with a constant sum of distances to two foci. |
| Hyperbola | Two opposing curves with a constant difference of distances. |
| Asymptote | A line that guides and is approached by a curve. |
| Vertex | The point where the curve is most pronounced; midpoint for others. |
Conclusion
Conic sections are crucial for mastering AP® Precalculus, as they connect math theory with real-world applications. Learning these different shapes and equations not only enhances understanding but brings greater appreciation for the subject’s depth and utility. Remember, practice makes perfect, so keep working on those equations!
Sharpen Your Skills for AP® Precalculus
Are you preparing for the AP® Precalculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!
Need help preparing for your AP® Precalculus exam?
Albert has hundreds of AP® Precalculus practice questions, free response, and an AP® Precalculus practice test to try out.









