Coulomb’s Law is not just an important concept in AP® Chemistry; it’s a pretty central concept in physics as well. Fortunately, that probably means that you’re pretty familiar with the basics already. In this installment of the AP® Chemistry Crash Course, we’ll start by going over the basic principles of Coulomb’s Law (even if you think you know it, skim it anyways — it’s a good review), and then we’ll go over how Coulomb’s Law relates to chemistry.

First of all, let’s go over the fundamental physics. Opposite charges attract, and like charges repel. In the context of subatomic particles, this boils down to protons repel protons, electrons repel electrons, and protons attract electrons (and of course, vice versa).

While that’s good enough for a basic explanation, we’ll need to dive a little bit into the minutiae. Here is the scalar Coulomb equation:

F=k\dfrac{q_1q_2}{r^2}

Let’s go over the equation term by term.

F: This is the force exerted by one of the charged particles on the other. The force exerted by one particle on another is equal in both directions (Newton’s Third Law).

k: This is Coulomb’s constant; we don’t have to worry much about that since it doesn’t really come up in chemistry. Leave that to the physicists.

q_1 and q_2: These are the magnitudes of the charges involved. If we’re dealing with simple electrons and protons, these will be 1; however, if we’re dealing with an atomic nucleus (for example), the magnitude will be equal to the number of protons in the nucleus. Basically, it’s just the charge number of the particle, whatever it is.

r: This is the distance between the particles. Note the squared term. This is sometimes referred to as the “inverse-square law”.

What Can We Take Away from this Equation?

1. The force is proportional to the magnitude of both charges.

2. The force is inversely proportional to the square of the distance between the two charges.

3. If the two charges have the same sign (positive or negative), the force is repulsive; if they have different signs, the force is attractive (this is not from the equation).

Does that all make sense? Let’s move on to the chemistry.

Why does Coulomb’s Law matter? Well, in an atom, you have the nucleus (held together by the strong force, which we don’t need to worry about) and the electrons moving around it. What keeps those electrons from leaving the atom? They are attracted to the protons in the nucleus, as Coulomb’s Law predicts. The minutiae of Coulomb’s Law (i.e., inverse-squared law, magnitude of charges) will become relevant as we move into applications.

The major application of Coulomb’s Law in AP® Chemistry is in calculating ionization energy. Ionization energy is (as the name would imply) the energy needed to make an atom into an ion by removing an electron.

Why is this related to Coulomb’s Law? The protons in the nucleus attract the electrons, so taking away an electron will require some energy to overcome that Coulombic attraction.

Naturally, all other things being equal, we would expect a higher ionization energy to correspond with a larger nucleus, since that larger nucleus would have more protons and thus more positive charge. And in fact, that is one effect that we see (we’ll look at a diagram in a moment).

However, we also see an effect mediated by the r term: distance. You see, because of quantum mechanics, electrons orbit the nucleus in discrete shells. You’ve almost certainly encountered them already: 1s^2, 2s^2, 2p^6, etc. So, in nitrogen, for example, we’ll have two electrons in the inner shell, and five electrons out in the second shell (two of which are in the 2s shell and three of which are in the 2p shell).

Because the distance is greater to the electrons in the outer shells, Coulomb’s Law dictates that the ionization energy will be lower. It’s important to note, however, that though the 2s electrons and 2p electrons may appear to be in the same shell, the 2p electrons are slightly farther out, so their ionization energy will be slightly lower.

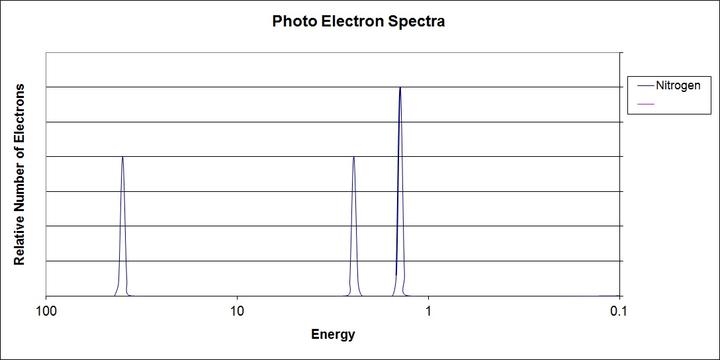
Enough with the theory — let’s look at a simplified ionization energy chart for nitrogen (atomic number 7).

Some context for what this diagram means: the most common way to look at ionization energies is though photoemission spectroscopy. Essentially, we fire photons of a certain energy at an element (such as nitrogen) and we see how many electrons come out of the element.

This effect is known as the photoelectric effect, and it’s actually the theory that won Einstein the Nobel Prize. We also now use this effect to create streams of electrons, or current, from photons: in other words, this is how solar panels work.

The important idea underlying photoemission spectroscopy (sometimes called photoelectron spectroscopy) is that if an atom is struck by a photon with at least the same amount of energy as specified by the ionization energy, then the atom will be ionized; however, if the photon does not have enough energy, the atom will not be ionized, even if it’s struck by millions of low-energy photons.

What does this mean for photoemission spectroscopy? Essentially, we can pin down what the ionization energies are for that atom because below that energy, nothing will happen, and above that energy, many electrons will be knocked off.

With that in mind, let’s look at the diagram again.

As you can see, there are three large peaks, two approximately equal in height, and one about one and a half times taller over to the right side. What does this mean?

As they are labeled, the two smaller peaks denote the four electrons in the inner s shells (two each). The 1s shell is the closest to the nucleus of the atom, so naturally, those electrons have the highest ionization energy. Pay close attention to the x-axis, because it doesn’t go in the direction we’re used to. The left-most side actually has the most energy, and the rightmost side has the least.

The 2s shell is next in line. It’s somewhat further away from the nucleus, so the ionization energy of its two electrons is lower.

Lastly, we have the 2p shell. Being the furthest away from the nucleus, its electrons have the least ionization energy. However, it’s important to note the size of this peak. Nitrogen normally has seven electrons; four of these are in the 1s and 2s shells. The remainder of the electrons are in the 2p shell. Because there are three rather than two electrons in the 2p shell, the peak at that energy is one and a half times larger than the other two peaks.

Does That All Make Sense?

Let’s review the basics of what you’ve learned (and if you’re just skimming this article, check here to see if you actually understood any of it):

1. Coulomb’s Law. Like charges repel; opposite charges attract. The force is proportional to the magnitude of the charges and inversely proportional to the square of the distance between them.

2. Ionization energy, an application of Coulomb’s Law. Position of the peaks in the PES graph horizontally denotes which shell the electrons are in; size of the peaks vertically denotes how many electrons are in that shell.

3. Photoemission spectroscopy (PES). Photons of a certain wavelength are fired into atoms of an element and either knock off electrons or don’t depending on whether they exceed the requisite ionization energy.

Now, for the part you’ve all been waiting for. Will this be on the test?

Absolutely, but the problems you may see will require more than simple memorization of rules. Here’s an example.

Which Has a Higher First Ionization Energy, Li or Na?

First, let’s make sure that we understand the question. A first ionization energy, as the name implies, is the energy required to remove the first of the electrons from the atom. In the diagram above, the first ionization energy would be a bit more than 1, since that electron would be the easiest to take off.

So which would have a higher first ionization energy, Li or Na? Well, let’s look at their shell structures. Li has three electrons, so its structure would be 1s^2, 2s^1. Na has eleven electrons, so its structure would be 1s^2, 2s^2, 2s^6, 3s^1.

That’s certainly not a hard problem, though it does take a little thinking. All you have to do is remember Coulomb’s Law and apply it to the atoms in question, and you’ll do fine with all the Coulomb’s Law questions the exam can throw at you. Good luck!

Looking for AP® Chemistry practice?

Kickstart your AP® Chemistry prep with Albert. Start your AP® exam prep today.