Looking to understand the different forms of quadratic equations? Read below for an explanation of the three main forms of quadratics (standard form, factored form, and vertex form), examples of each form, as well as strategies for converting between the various quadratic forms.

Your mathematics journey has taken you far. There was a time when the words “variable” and “equation” were only concepts you would someday understand. The skills you developed then gave you a foundation of using mathematics to solve simple problems. Then, you delved into variables and unknown values. You conquered solving equations for the value of x. You are able to create and interpret graphs of equations.
Now, we are opening a new tool: quadratics! Quadratic equations may feel different, scary, exciting, or all of the above. Regardless of how you feel going into learning quadratic equations, know that you can conquer this, too. You are entering a new level of mathematical understanding and a new world of real-life situations to model. Let’s get started!
What We Review
The 3 Forms of Quadratic Equations
There are three commonly-used forms of quadratics:
| 1. Standard Form: y=ax^2+bx+c 2. Factored Form: y=a(x-r_1)(x-r_2) 3. Vertex Form: y=a(x-h)^2+k |
Each quadratic form looks unique, allowing for different problems to be more easily solved in one form than another. We will unpack the features of each form and how to switch between forms.
Return to the Table of Contents
Why are There Forms of Quadratic Equations?
Each form of a quadratic equation includes specific advantages. Recognizing the benefits of each different form can make it easier to understand and solve different situations.
What Does the Standard Form of a Quadratic Tell You?
Let us begin with the benefits of standard form. In standard mathematical notation, formulas and equations are written with the highest degree first. The degree refers to the exponent. In the case of quadratic equations, the degree is two because the highest exponent is two. Following the x^2 term is the term with an exponent of one followed by the term with an exponent of zero.
| Standard Form of Quadratic Equation: y=ax^2+bx+c |
The benefits of standard form include quickly identifying the end behavior of a function and identifying the values of a, b, and c.
The end behavior of a function is identified by the leading coefficient and the degree of a function. The degree of a quadratic equation is always two. The leading coefficient of a quadratic equation is always the term a when written in standard form.
If the value of a is positive, the parabola opens up, meaning the function rises to the left and rises to the right. If the value of a is negative, the parabola opens down, meaning the function falls to the left and falls to the right.
y=3x^2+2x-1
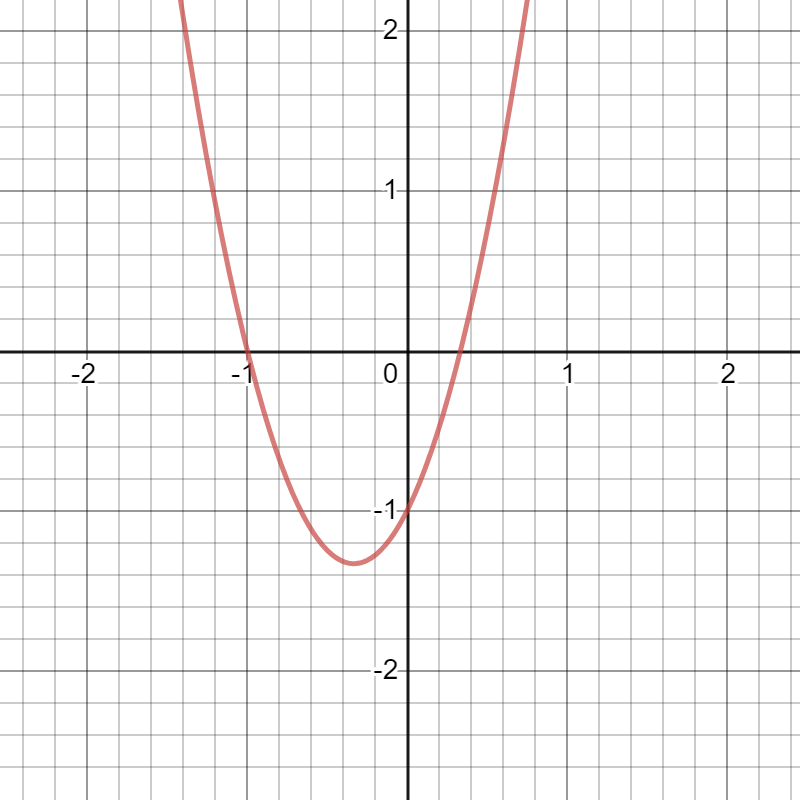
Notice: positive a value, degree of 2, parabola opens “up”
y=-3x^2+2x+1
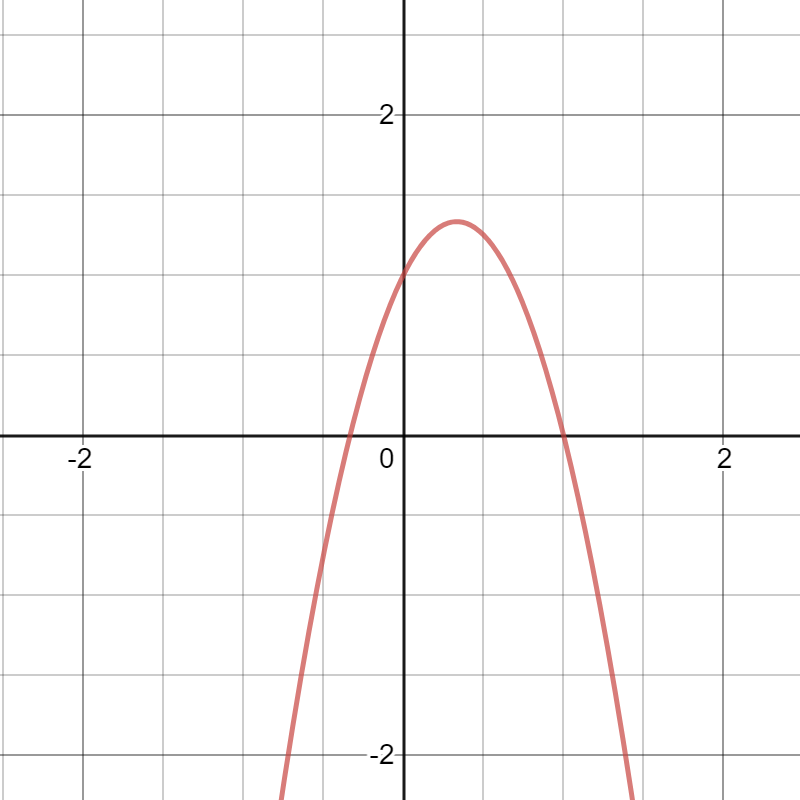
Notice: negative a value, degree of 2, parabola opens “down”
One method for solving a quadratic equation is to use the quadratic formula. To do so, we must identify the values of a, b, and c. To learn more about this, read our detailed review article on the quadratic formula.
What Does the Factored Form of a Quadratic Tell You?
Next, let’s now consider why factored form is useful. To get to factored form, we do exactly what it sounds like: we factor the equation from standard form.
| Factored Form of Quadratic Equation: y=a(x-r_1)(x-r_2) |
In the factored form of a quadratic, we are also able to determine end behavior using the value of a. Although the degree is not as easily identifiable, we know there are only two factors, making the degree two. The end behavior follows the same rules explained above.
The additional benefit of factored form is identifying zeros, or x-intercepts, of the function. The value of r_1 and the value of r_2 are both zeros (also called “solutions”) of the quadratic function.
y= - (x + 2)(x - 3)
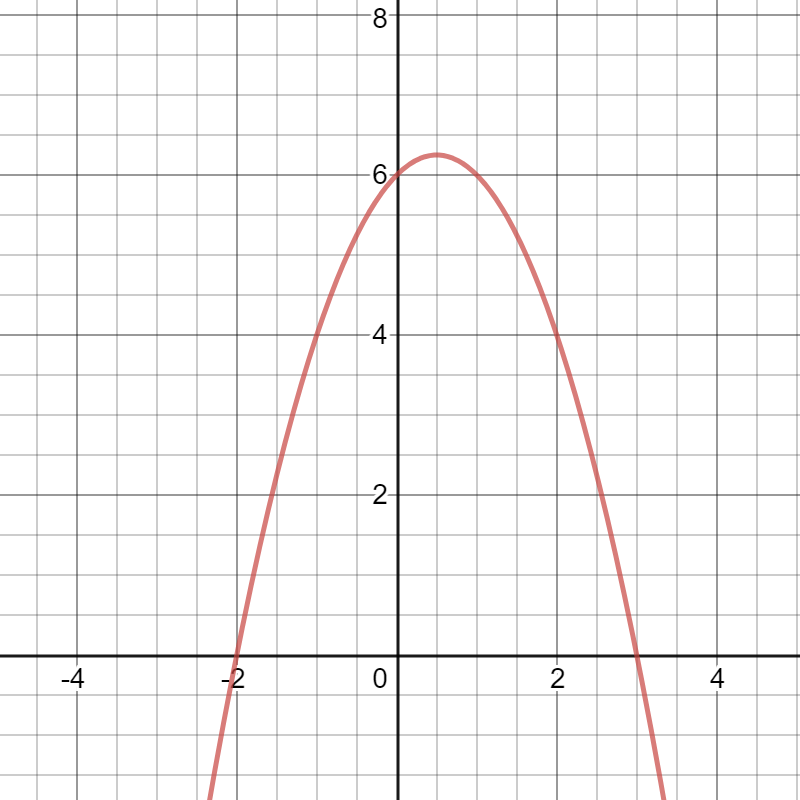
Zeros: x = -2 \text{ and } x= 3
We must note that not all quadratics have “real” zeros (some quadratics require imaginary numbers as their zeros), so factored form may not always be applicable.
What Does the Vertex Form of a Quadratic Tell You?
Finally, we have the vertex form of a quadratic. Remember, the vertex is the point where the axis of symmetry intersects the parabola. It is also the lowest point of a parabola opening up or the highest point of a parabola opening down.
| Vertex Form of Quadratic Equation: y=a(x-h)^2+k |
As you may expect, the main benefit of vertex form is easily identifying the vertex. The vertex of a parabola, or a quadratic equation, is written as (h,k) where the h is the x-coordinate and the k is the y-coordinate.
As we can see, the value of h and the value of k are easily identifiable in this form. Additionally, we can still determine the end behavior using the value of a.
y= 3(x-2)^2 - 1
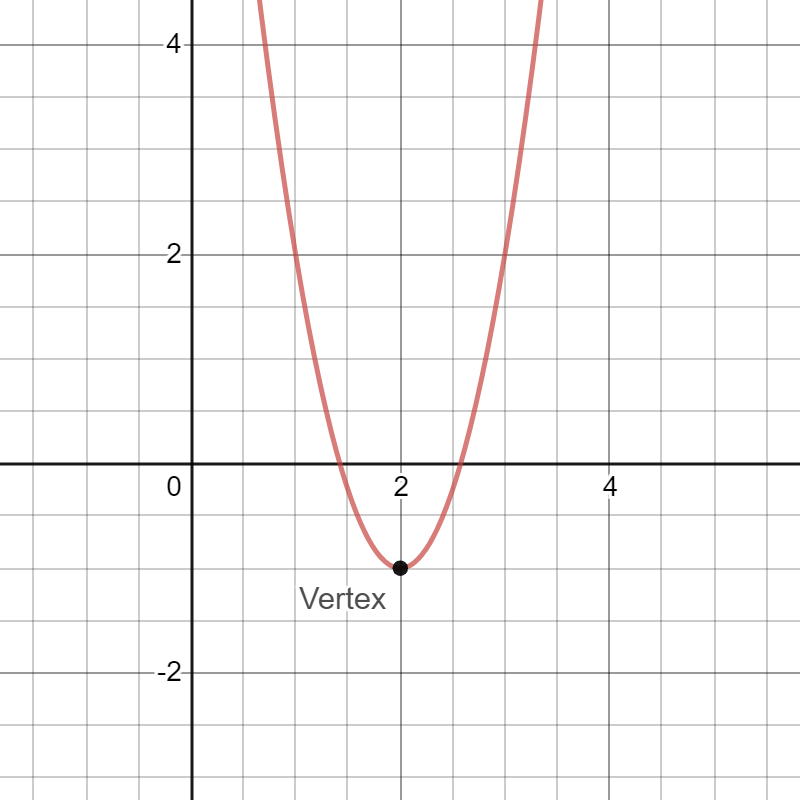
Vertex: (2,-1)
Return to the Table of Contents
What is the Standard Form of a Quadratic?
| Standard Form of Quadratic Equation: y=ax^2+bx+c |
Remember, standard form provides us values for the coefficients a, b, and c, while x and y are the variables.
For example, the equation:
y=3x^2+7x-9
…is in standard form, telling us that a=3, b=7, and c=-9.
What is the Factored Form of a Quadratic?
| Factored Form of Quadratic Equation: y=a(x-r_1)(x-r_2) |
In factored form, we can see the zeros, also called x-intercepts, are r_1 and r_2. Our variables remain x and y, and a is a coefficient.
In the factored form equation:
y=3(x+8)(x-6)
…the two x-intercepts are -8 and 6, and the value of a equals 3.
What is the Vertex Form of a Quadratic?
| Vertex Form of Quadratic Equation: y=a(x-h)^2+k |
In vertex form, the variables x and y and the coefficient of a still remain, but now we can identify the vertex using the values of h and k.
For instance, in the equation:
y=-7(x-2)^2+16
…which is in vertex form, the vertex is (2,16) and the value of a is -2.
Converting Between Forms of Quadratic Equations
Often, we need many different pieces of information about quadratic equations. It can be useful to see the same quadratic equation in the multiple forms. Just like a chameleon can change colors in different situations, we can change the forms of quadratics to suit our needs.

Change forms of a quadratic like a chameleon!
The ability to switch between forms quickly and accurately enables us to understand the quadratic equation well and easily identify needed pieces of information. For example, you may be asked to determine the zeros of a quadratic equation given in standard form. In order to identify the zeros, we first must change the equation to factored form.
Return to the Table of Contents
Convert from Standard Form to Factored Form
Let us begin with the equation:
y=x^2+5x-24
We may be asked for the zeros of the equation. In order to determine the zeros, we can change this into factored form. To change this into factored form, we must factor the expression x^2+5x-24. Let’s remember what Factored Form looks like:
| Factored Form of Quadratic Equation: y=a(x-r_1)(x-r_2) |
In order to factor the expression, we must determine the factors of -24 that have a sum of 5. We can list the factors of -24 and their sums:
| Factors | Sum of Factors |
|---|---|
| -24 and 1 | -24 + 1 = -23 |
| -1 and 24 | -1 + 24 = 23 |
| -12 and 2 | -12 + 2 = -10 |
| -2 and 12 | -2 + 12 = 10 |
| -6 and 4 | -6 + 4 = -2 |
| -4 and 6 | -4 + 6 = 2 |
| -8 and 3 | -8 + 3 = -5 |
| -3 and 8 | -3 + 8 = 5 |
The two values that multiply to -24 and have a sum of 5 are -3 and 8. Therefore, we can rewrite our quadratic equation by factoring.
y=x^2+5x-24
y=(x-3)(x+8)
To determine the zeros, we set the equation equal to zero. Then, we can solve by setting each factor equal to zero:
(x-3)(x+8)=0
x-3=0
x=3
x+8=0
x=-8
Therefore, the zeros of the function are 3 and -8. The final factored form the equation is:
y=(x-3)(x+8)
To learn more about this approach by reading our article on solving quadratic equations by factoring.
Return to the Table of Contents
Convert from Standard Form to Vertex Form
Instead of being asked for the zeros, we could be asked for the vertex of a quadratic equation. Let us begin with the quadratic equation:
y=x^2+6x-5
…which is given in standard form, and determine the vertex of the equation. In order to do so, we will convert this into vertex form.
To convert into vertex form, we must complete a process called “completing the square”. Essentially, we are setting up a trinomial that we can factor into a perfect square. Let us remember what vertex form of a quadratic looks like:
| Vertex Form of Quadratic Equation: y=a(x-h)^2+k |
We need to set up the equation just right so that we can factor it to create (x-h)^2. This may sound intimidating, but there is a step-by-step process that always works!
First, isolate the x. This means we need to move any constants to the side with y. Constants are terms with no variable attached.
y=x^2+6x-5
y+5=x^2+6x
If we had a leading coefficient other than one, we would divide all terms by the leading coefficient. Remember, the leading coefficient is the number in front of x^2. In our case, we have a leading coefficient of one, so we can skip this step.
From here, we need to determine what value to add to both sides. To determine this value, we look at the number in front of x. In our case, this value is 6. We have half of this value and then square the result.
\dfrac{1}{2} (6) = 3
3^2=9
The value we must add to both sides of our equation is 9. Remember this will create a trinomial which is a perfect square (thus, the name “completing the square”).
y+5=x^2+6x
y+5\textcolor{blue}{+9}=x^2+6x\textcolor{blue}{+9}
Now we have created a trinomial, x^2+6x+9, which we can factor into a perfect square. This factors into (x+3)^2. Notice this matches the step where we took half of 6. After we factor it, we will then solve for y.
y+5+9=x^2+6x+9
y+5+9=(x+3)^2
y+14=(x+3)^2
y=(x+3)^2-14
Now that the equation is in vertex form, we can identify the vertex as (-3,-14). The vertex form of the quadratic equation is:
y=(x+3)^2-14
Converting from quadratic form to standard form is quite common, so you can also check out this helpful video for another example.
Return to the Table of Contents
Convert from Factored Form to Standard Form
To convert an equation from factored form into standard form simply involves multiplying the factors. For example, let us change the quadratic equation:
y=(3x-2)(-x+7)
…into standard form. We will use double distribution to multiply the factors (3x-2) and (-x+7) together.
y=(3x-2)(-x+7)
y=(3x \times -x) + (3x \times 7) + (-2 \times -x) + (-2 \times 7)
y=-3x^2+21x+2x-14
y=-3x^2+23x-14
Therefore, the standard form of the quadratic equation is y=-3x^2+23x-14.
Return to the Table of Contents
Convert from Vertex Form to Standard Form
Finally, we may also need to convert an equation from vertex form into standard form. For example, we can change the equation:
y=2(x+7)^2-10
…into standard form. We will expand the expression (x+7)^2 and again use double distribution. Then, we will continue simplifying the equation.
y=2(x+7)^2-10
y=2(x+7)(x+7)-10
y=2(x^2+14x+49)-10
y=2x^2+28x+98-10
y=2x^2+28x+88
Therefore, the standard form of the quadratic equation is y=2x^2+28x+88.
Return to the Table of Contents
Practice with Forms of Quadratics
For some practice questions covering the forms of quadratics, check out Albert’s Algebra 1 practice course! All of Albert’s questions include explanations of solutions and how to avoid common mistakes.
Additionally, licensed Albert teachers can assign students this short Algebra 1 Topic Quiz that focuses on vertex, roots, and the various forms of quadratics.
Finally, check out our other detailed Algebra 1 review guides to learn more about quadratic.








