Free fall and projectile motion describe objects that are moving through the air and acted on only by gravity. In this post, we will describe this type of motion using both graphs and kinematic equations. Since projectile motion involves two dimensions, these problems can be complex. We will explain many examples so you can see how to solve different types of projectile motion. 

Free Fall

An object that is moving under only the influence of gravity is in free fall. In order for an object to be in free fall, wind and air resistance must be ignored. On Earth, all objects in free fall accelerate downward at the rate of gravity or 9.81\text{ m/s}^2.

Applying Free Fall to Kinematic Equations

When analyzing free fall motion, we can apply the same kinematic equations as we did for motion on the ground. We can then use these equations to determine properties such as distance, time, and velocity. 

How to Find Distance Fallen for an Object in Free Fall

If an object is in free fall, we can use kinematic equations to find the distance it falls during a certain time. You will typically use the following kinematic equation to calculate the distance fallen:

Formula for Finding Distance if Time is Known d=v_i t+\frac{1}{2}at^2

In order to use this equation, you need to know the initial velocity of the object and the time of flight. Remember that the acceleration of a free falling object is always equal to the acceleration due to gravity, 9.81\text{ m/s}^2. 

Many free fall physics problems will include scenarios where objects are dropped from rest. In this case, the initial velocity is zero and the first term of the kinematic equation above will cancel out. 

If the time is not known, another method for calculating the distance fallen is to use the following kinematic equation:

Formula for Finding Distance when Time in Unknown v_f^2=v_i^2 + 2ad

In this case, you must know the final velocity v_f of the object. Then, you can solve the equation for the distance d.

How to Find Time for an Object in Free Fall

The amount of time an object is in free fall will depend on its velocity and the distance it falls. Similar to distance, there are two equations you can use to find the time, depending on what you know. 

If you know the initial and final velocity of the object, then the simplest way to calculate time is using the kinematic equation:

Formula for Finding Time Using Velocities v_f=v_i+at

This equation can be solved for time. Then, you’ll only need to substitute the values for the velocities and the acceleration due to gravity.

Another method to find time if you do not know the object’s final velocity is to use the equation:

Formula for Finding Time Using Distance d=v_i t+\frac{1}{2}at^2

Note that in this equation there are two terms that include the time t. Unless the initial velocity is zero, this can make it more challenging to solve this equation for time. If using this equation, you may need to use the quadratic formula to solve for time.

How to Find Final Velocity for an Object in Free Fall

The final velocity of an object in free fall depends on the amount of time it falls. Due to the acceleration of gravity, the velocity will increase every second by 9.81\text{ m/s}. The final velocity can be calculated using the equation:

Formula for Finding Velocity Using Time v_f=v_i+at

If you do not know the amount of time the object is falling, another method for calculating the final velocity is using the kinematic equation: 

Formula for Finding Velocity Using Distance v_f^2=v_i^2 + 2ad

This equation requires that you instead know the distance that the object falls. If you are using this equation to find the final velocity, remember that the final velocity is squared in this equation. That means you will need to take a square root as your final step to solve for the final velocity. 

Examples of Free Fall

In this next section, we’ll apply the methods you just learned to solve some problems about free fall motion.

Example 1: How to Find the Distance for an Object Dropped from Rest

For example, an object is dropped from rest from the top of a tall building. It hits the ground 5\text{ s} after it is dropped. What is the height of the building? 

In this scenario, we know that the object’s initial velocity is zero because it was dropped from rest. We also know that the acceleration is 9.81\text{ m/s}^2. This problem is asking us to find the distance the object falls. This will be equal to the height of the building.

Based on this information, we can use the following kinematic equation to find the distance:

d=v_i t+\frac{1}{2}at^2

Substituting the given values produces:

d=(0\text{ m/s})(5\text{ s})+\frac{1}{2}(9.81\text{ m/s}^2)(5\text{ s})^2

d=122.625\text{ m}

Therefore, the height of the building is about 123\text{ m}.

Example 2: How to Find the Final Velocity for an Object with Initial Velocity

In another example, an object in free fall has an initial, downward velocity of 2\text{ m/s} and falls a distance of 45\text{ m}. What is the object’s final velocity? 

In this scenario, we are given the object’s initial velocity, v_i and the distance d. We also know that the acceleration is 9.81\text{ m/s}^2. Based on this information, we can use the following kinematic equation to find the final velocity:

v_f^2=v_i^2 + 2ad

Substituting the given values produces:

v_f^2=(2\text{ m/s})^2+2(9.81\text{ m/s}^2)(45\text{ m})

Since the initial velocity is in the same direction as the acceleration (downward) we can use the same sign for both values.

v_f^2=886.9\text{ m}^2\text{/s}^2

Our last step is to eliminate the square by taking the square root:

v_f=\sqrt{886.9\text{ m}^2\text{/s}^2}

v_f=29.78\text{ m/s}

Therefore, the final velocity of the object is about 30\text{ m/s}.

Motion Graphs for Objects in Free Fall

In addition to using physics equations, we can also represent free fall motion with motion graphs. Position-time graphs, velocity-time graphs, and acceleration-time graphs can tell us a lot about the object’s motion over time. Want a more in-depth review of motion graphs? Check out this blog post!

Position-Time Graph for an Object in Free Fall

In terms of position, many objects in free fall start at a high position, or height off the ground, and move downward. Objects in free fall accelerate due to gravity. Therefore, the position-time graph for free fall motion must be curved. This means that objects in free fall start with a slow velocity and gradually speed up which is represented by the steep downward curve of the graph. 

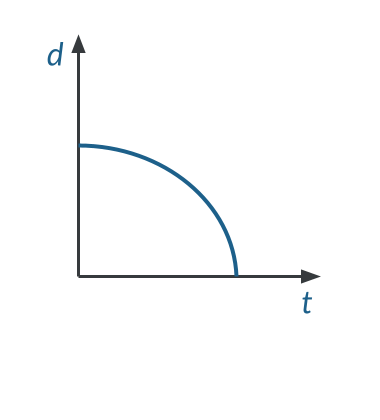
Velocity-Time Graph for an Object in Free Fall

As an object falls, its velocity increases due to the acceleration of gravity. This means that the velocity starts slow and steadily increases in the downward direction. The graph below shows the velocity-time for an object in free fall:

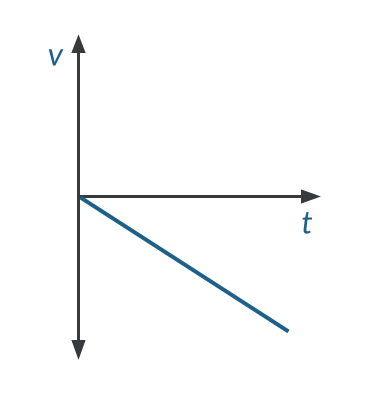
Note that the slope of this graph is constant and represents the acceleration due to gravity, or -9.81\text{ m/s}^2.

Acceleration-Time Graph for an Object in Free Fall

Free fall acceleration is constant. Throughout the entire time that an object is falling, it is accelerating at a rate equal to the acceleration due to gravity, -9.81\text{ m/s}^2. As shown in the graph below, the acceleration-time graph is a constant negative line. 

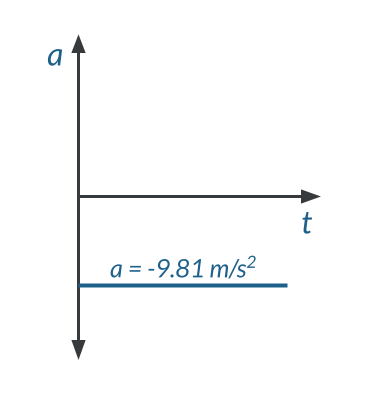
Projectile Motion

A projectile is an object that is launched or thrown into the air and then only influenced by gravity. Projectile motion has many similarities to free fall motion, however, projectiles may also travel a horizontal distance in addition to falling vertically down. 

Examples of Projectile Motion

The exact trajectory, or path, a projectile will take depends on how it is launched. However, all projectiles follow a curved trajectory such as in the image shown below:

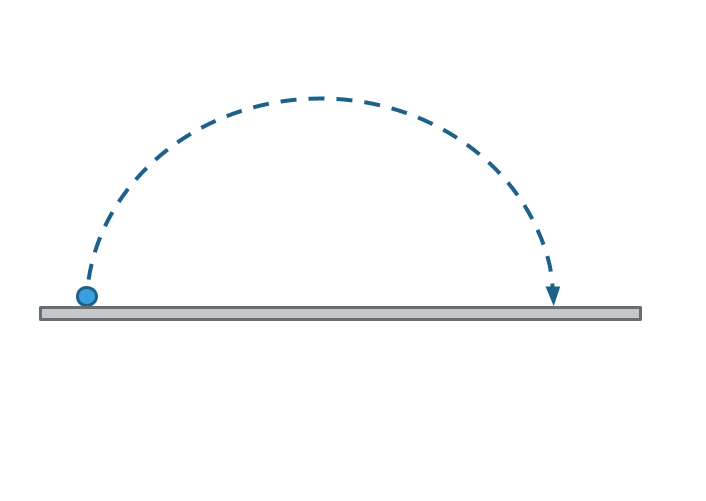
If you play or watch sports, you likely have already observed projectile motion. Projectile motion describes the arc of a basketball in a free throw, a fly ball in baseball, or a volleyball bumped over the net. 

Horizontal Component of Velocity

To analyze projectile motion, we must separate the motion into horizontal and vertical components. The horizontal component of a projectile’s velocity is independent of the vertical component of velocity. Since gravity acts vertically, there are no horizontal forces acting on projectiles. This means that the horizontal component of a projectile’s velocity remains constant throughout the entire flight. 

Example: Finding the Horizontal Component

For example, a projectile is launched from the ground with an initial speed of 8\text{ m/s} at a 60^{\circ} angle. What is the horizontal component of the projectile’s velocity?

We will need to use trig identities to determine the components of the velocity. We can visualize the components as a triangle where the hypotenuse is the initial velocity and the sides represent the horizontal, v_{ix}, and vertical, v_{iy}, components of the velocity.

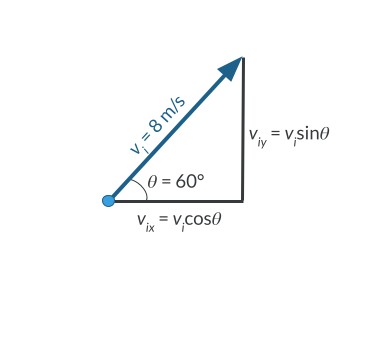
Cosine is defined as the adjacent side of the triangle divided by the hypotenuse. Since the horizontal component is adjacent to the angle, we can use cosine to find the horizontal component of velocity:

v_{ix}=v_i\cos\theta=(8\text{ m/s})\cos(60^{\circ})

v_{ix}=4\text{ m/s}

Therefore, the horizontal component of the initial velocity is 4\text{ m/s}.

Need to review your trig identities? Try out this resource from Khan Academy.

Vertical Component of Velocity

The vertical component of a projectile’s velocity will be influenced by gravity, which acts vertically on the object causing it to accelerate downward. Therefore, the vertical component of velocity will change throughout the projectile’s flight. We can calculate the vertical component of velocity at a particular time in a method similar to calculating the horizontal component. 

Example: Finding the Vertical Component

In the same example, a projectile is launched from the ground with an initial speed of 8\text{ m/s} at a 60^{\circ} angle. What is the vertical component of the projectile’s velocity?

As we visualize the velocity components, we are solving this time for the opposite side of the triangle. Sine is defined as the opposite side of the triangle divided by the hypotenuse. Therefore, the initial vertical velocity is:

v_{iy}=v_i\sin\theta=(8\text{ m/s})\sin(60^{\circ})

v_{iy}=6.9\text{ m/s}

Solving Projectile Motion Questions

Let’s apply what we’ve learned to some examples of projectile motion!

Example 1: Finding the Range of a Projectile

In this example, a projectile is fired horizontally with a speed of 5\text{ m/s} from a cliff with a height of 60\text{ m}. How far from the base of the cliff will the projectile land? 

In this scenario, we are given the initial horizontal velocity v_{ix}=5\text{ m/s} and the vertical change in position d_y=-60\text{ m}. Since the projectile is launched horizontally, the initial vertical velocity, v_{iy}, is zero. We also always know in projectile motion that the vertical acceleration is a_y=-9.81\text{ m/s}^2 and the horizontal acceleration, a_x, is zero.

This problem is asking us to find the horizontal displacement, or d_x. This is also referred to as the range. We can use the following kinematic equation to find the projectile’s final horizontal position:

d_x=v_{ix} t+\frac{1}{2}a_xt^2

Since the horizontal acceleration of a projectile is zero, this equation can be simplified to:

d_x=v_{ix} t

Before we can solve this equation, we must first determine the time of the projectile’s flight. We can actually use this same equation in the vertical direction to solve for time:

d_y=v_{iy} t+\frac{1}{2}a_yt^2

Since the initial vertical velocity is zero, this equation can be simplified to:

d_y=\frac{1}{2}a_yt^2

Solving for t:

2d_y=a_yt^2

t^2=\dfrac{2d_y}{a_y}

t=\sqrt{\dfrac{2d_y}{a_y}}

Substituting the given values:

t=\sqrt{\dfrac{2(-60\text{ m})}{-9.81\text{ m/s}^2}}

t=3.5\text{ s}

Now we can use this time to calculate the horizontal displacement of the projectile:

d_x=v_{ix} t

d_x=(5\text{ m/s})(3.5\text{ s})=17.5\text{ m}

Therefore, the projectile will land about 17.5\text{ m} from the base of the cliff. 

Example 2: Finding the Maximum Height of a Projectile

As another example, a projectile is launched from the ground with an initial velocity of 25\text{ m/s} at an angle of 50^{\circ}. What is the projectile’s maximum height?

As a projectile travels upward, its vertical velocity becomes slower and slower due to the negative acceleration of gravity. At the maximum height of the trajectory, the projectile’s vertical velocity will momentarily be zero as the projectile stops and turns to move downward. Therefore, in this scenario, our final vertical velocity, v_{fy}, is zero.

We can use the following kinematic equation to solve for the maximum height, d_y:

v_{fy}^2=v_{iy}^2 + 2a_y d_y

Solving for d_y:

d_y=\dfrac{v_{fy}^2-v_{iy}^2}{2a_y}

Before we can use this equation to calculate the height, we will need to use the sine trig identity to find the vertical component of the initial velocity:

v_{iy}=v_i\sin\theta

v_{iy}=(25\text{ m/s})\sin(50^{\circ})=19.15\text{ m/s}

Since the initial velocity is in the opposite direction as the acceleration, it’s really important to remember the sign here. If we define moving up as positive, then the initial velocity is positive and the acceleration is negative. Substituting this initial vertical velocity and the given values into the equation above gives:

d_y=\dfrac{v_{fy}^2-v_{iy}^2}{2a_y}

d_y=\dfrac{(0\text{ m/s})^2-(19.15\text{ m/s})^2}{2(-9.81\text{ m/s}^2)}

d_y=18.7\text{ m}

Therefore, the projectile will reach a maximum height of about 18.7\text{ m}.

For more examples and an explanation of solving these types of projectile motion problems, check out this youtube video from Professor Dave. 

Conclusion

Understanding free fall and projectile motion allows you to solve some of the most complex problems you will encounter in introductory physics. All projectiles are acted on only by gravity, and the vertical and horizontal components of motion are independent of each other. This allows us to apply our kinematic equations to solve for a projectile’s time of flight, velocity, and displacement in each direction.