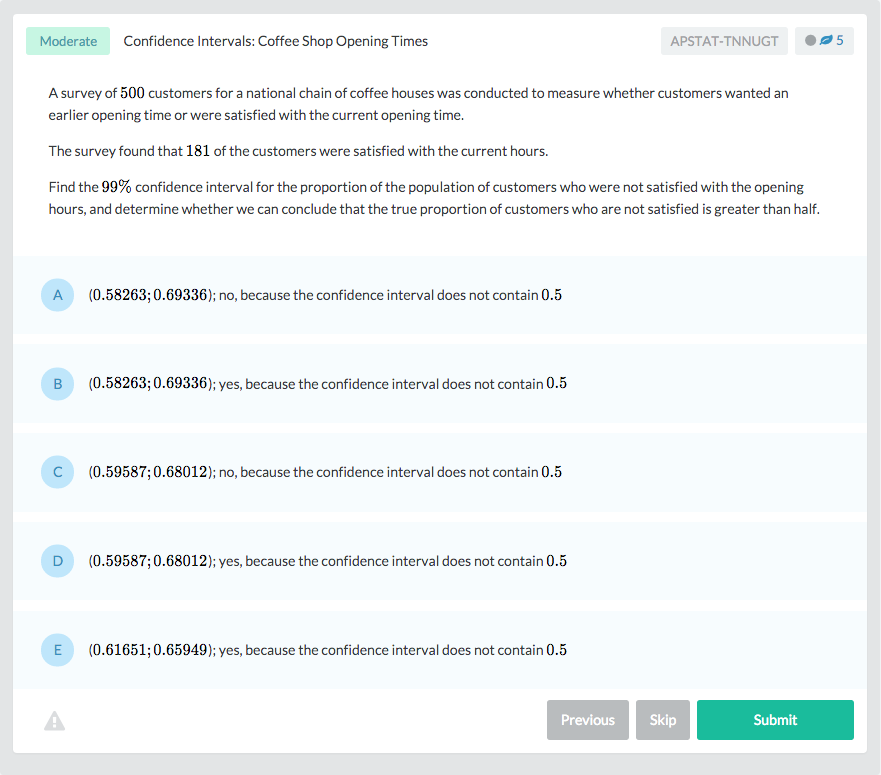
What is the German Tank Problem?
The German Tank Problem is a famous statistical problem that helped the Allied Forces during World War II, and can help you with your AP® Statistics review.
Statisticians use estimators when dealing with samples from a larger population. Often, it can be useful to know the size of the total population when you are working with a limited sample size from a population of unknown size. Estimating the total population size, or population maximum, can let you draw more accurate conclusions about the sample and how it represents or fails to represent the entire population. The German Tank Problem will help you do just that.
In World War II, each manufactured German tank or piece of weaponry was printed with a serial number. Using serial numbers from damaged or captured German tanks, the Allies were able to calculate the total number of tanks and other machinery in the German arsenal.
Allied mathematicians were only able to collect a limited sample of German tanks, but used that sample as an estimator of the population maximum of German tanks. They applied the same principles to estimating number and importance of factories, as well as a number of other manufactured munitions. Statistical analysis proved far more accurate than estimates based on conventional intelligence gathering, which tended to wildly overestimate the number of tanks produced each month.
For example, traditional intelligence gathering put production of tanks at an absurdly high 1,400 tanks per month. When statisticians calculated the population maximum, their estimate was a mere 256 tanks per month. It turned out that the statisticians’ information was more accurate than the spies’: according to German records recovered after the war, they had produced 255 tanks for the month in question.
As you can probably imagine, this was tactically useful information. In fact, it was critical to the Allies’ plan for D-Day. The German Tank Problem has remained one of the most famous examples of applied mathematics in the twentieth century. Today, the German Tank Problem is used by many AP® Stats teachers to demonstrate how to estimate a population parameter.
The Problem with Samples and Estimators
Essentially, the German Tank Problem demonstrates how to estimate the size of an entire population given only a limited sample. There are several estimators we can use to guess at the size of the population when given only a sample. None of them yield very accurate results, as the following example will demonstrate.
Say you have a sample of five random serial numbers from a group with an unknown population maximum. We’ll say those serial numbers are 3, 21, 30, 87, and 115. For the purpose of this example, we’ll also say that the population maximum is 150 so that you can follow along more easily.
First, we can attempt to calculate the population maximum by doubling the maximum value of the sample. The maximum sample value, or highest value in the sample, is 115. Doubled, that gives us 230—not quite twice our real maximum population.
That method is far too inaccurate and tends to overshoot the population maximum. So is the method of using twice the mean value of the sample, but it tends to have the opposite problem of underestimation. The mean of our example sample 51.2. Doubled, that comes out to 102.4. It’s closer to our target of 150, but still off by about 32%.
Lastly, we come to the method of doubling the sample median. The median of this sample is 30; doubled, that comes to 60—a long way off from 150.
Simply put, none of these methods provides the kind of accuracy you’d need if you had to plan a battle. They all rely too heavily on which numbers you draw for your sample. While some samples might give you estimators that get fairly close to the real population maximum, these methods are too hit or miss for high-stakes applied math.
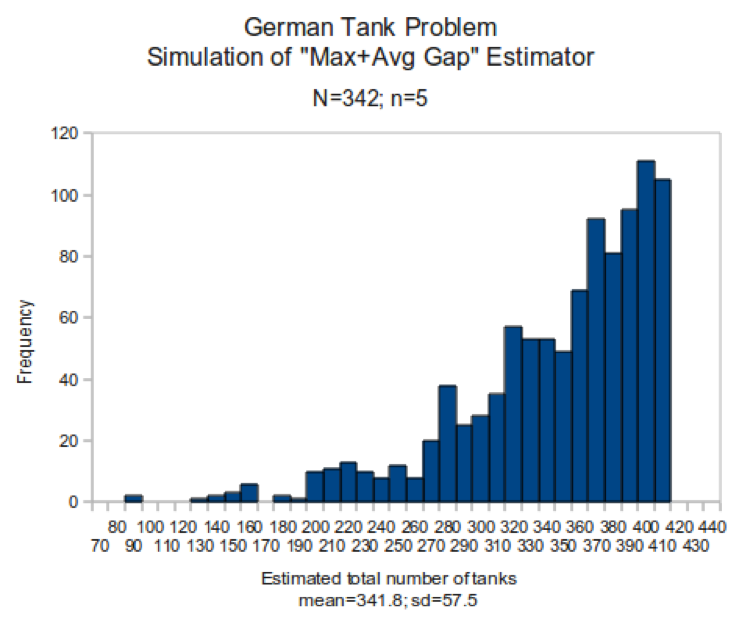
Image Source: Wikipedia Commons
How to Use the Minimum-Variance Unbiased Estimator (MVUE)
Fortunately, there’s a more accurate and relatively easy way to find an unbiased estimator. All you need to know is your sample size, the sample maximum (largest value in your sample), and this equation:
Population Maximum = Sample Maximum + (Sample Maximum / Sample Size) – 1
The MVUE equation solves the German Tank Problem by operating on the assumption that the population maximum is likely to be just a little higher than the sample maximum. That difference between sample maximum and population maximum is approximately equal to the mean gap between each number in the sample.
In our example, our sample size is 5 and our sample maximum is 115. Our equation would look like this:
Population Maximum = 115 + (115 / 5) – 1
That gives us an estimator of 137. In this particular sample, which I took by using a random number generator, we’re still off by about 9%. But compared to the methods demonstrated earlier, the Multi-Variable Unbiased Estimator estimated the maximum population within a margin of error of 10%. For an estimate based on only 5 numbers out of 150, that’s impressively accurate.
Wrapping Up the German Tank Question
For your AP® Stats test, you may have to solve problems similar to the German Tank Problem using the Multi-Variable Unbiased Estimator. As World War II demonstrated, there are many real-world applications for estimating the population maximum from your sample. You should be familiar with different estimators and be able to understand, and possibly explain for a free-response question, how and why the MVUE equation works.
Sampling distribution and parameters are groundwork concepts for introductory statistics, and an AP® level student should have a firm grasp of their relevance. For a teacher’s perspective on the application of sampling distribution, including its relation to the German Tank Problem and various other creative examples of its relevance, see this Special Focus published by the College Board.
Let’s put everything into practice. Try this AP® Statistics practice question:
Looking for more AP® Statistics practice?
Check out our other articles on AP® Statistics.
You can also find thousands of practice questions on Albert.io. Albert.io lets you customize your learning experience to target practice where you need the most help. We’ll give you challenging practice questions to help you achieve mastery of the ACT®.
Start practicing here.
Are you a teacher or administrator interested in boosting AP® Statistics student outcomes?
Learn more about our school licenses here.