What We Review
Introduction
Parametric equations might sound complex, but they’re just another way of representing curves. Instead of expressing a curve all at once, parametric equations use a parameter, typically labeled as ( t ), to define both the x and y coordinates. Understanding these graphs of parametric equations is key in Precalculus, as they help solve real-world problems involving motion and paths. Let’s talk about the most important topics from section 4.1 Parametric Functions in AP® Precalculus.
What are Parametric Equations?
Parametric functions consist of two separate equations for x and y, both depending on a third variable, the parameter ( t ). For instance:
- ( x(t) = f(t) )
- ( y(t) = g(t) )
In these equations, ( t ) represents the independent variable, while ( x ) and ( y ) are dependent on it. This format is incredibly flexible, allowing for effective modeling of various scenarios, like the trajectory of a moving object.
Constructing a Graph of a Parametric Function
Creating graphs of parametric equations involves several steps:
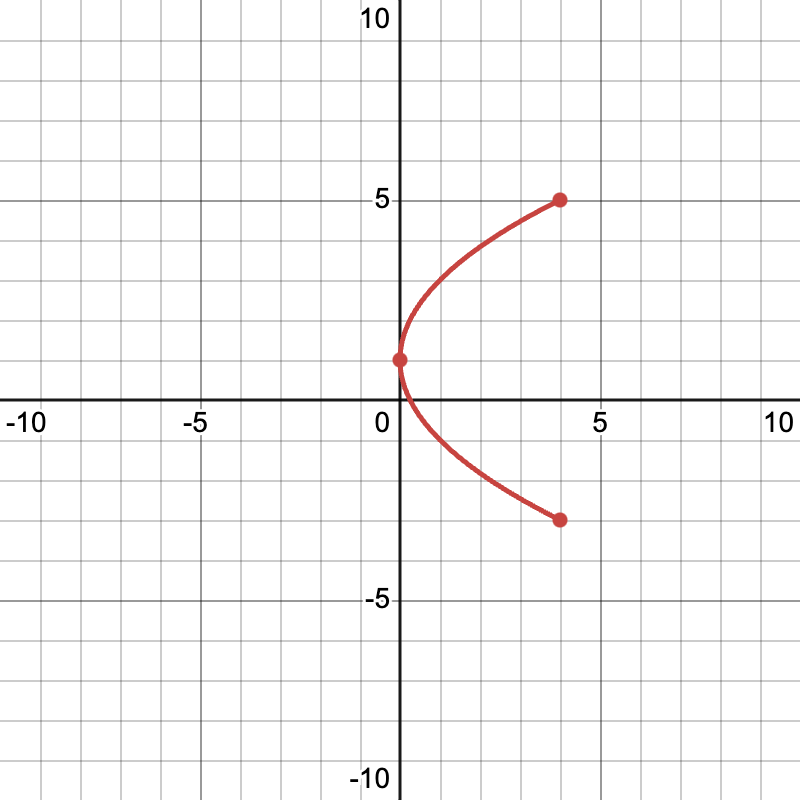
- Define the Parametric Equations: For example, let the equations be ( x(t) = t^2 ) and ( y(t) = 2t + 1 ).
- Generate a Numerical Table: Choose specific values for ( t ) and calculate corresponding ( x ) and ( y ).
- ( t = -2 ): ( x(-2) = 4 ), ( y(-2) = -3 )
- ( t = 0 ): ( x(0) = 0 ), ( y(0) = 1 )
- ( t = 2 ): ( x(2) = 4 ), ( y(2) = 5 )
- Plot the Points: Using the table, plot each point on a graph.
- Connect the Points: Draw a smooth curve through the points to represent the function.
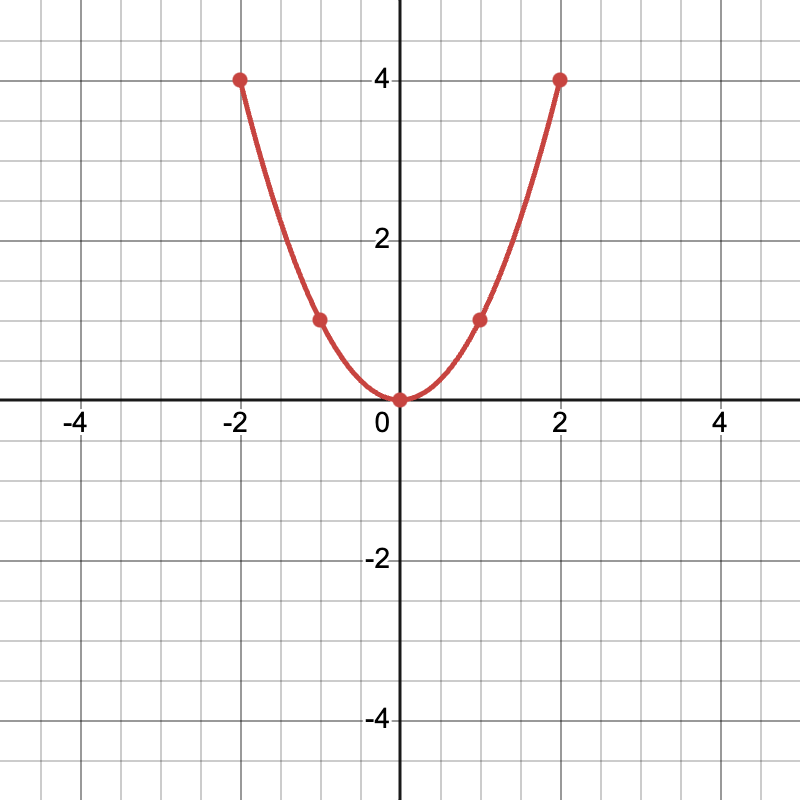
Example 1: Consider the parameters ( x(t) = t ) and ( y(t) = t^2 ). Let ( t = -2, -1, 0, 1, 2 ).
- Create the table:
| t | x(t)=t | y(t) = t^2 |
| -2 | -2 | 4 |
| -1 | -1 | 1 |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 2 | 2 | 4 |
- Plot and connect these: Observe a parabolic path opening upwards.
Understanding the Domain of Parametric Functions
The domain of parametric equations, concerning ( t ), influences where the graph starts and stops. For instance, a parameter restriction ( 0 \leq t \leq 2 ) indicates a segment of the entire curve.
Analyze the domain of ( x(t) = \cos(t) ), ( y(t) = \sin(t) ) for ( 0 \leq t \leq \pi ).
- The curve forms half a circle from the positive x-axis to the negative one.
Exploring Different Types of Parametric Curves
Parametric equations can graph many curve types, like circles or ellipses.
- Circle: Use ( x(t) = r \cos(t), y(t) = r \sin(t) ).
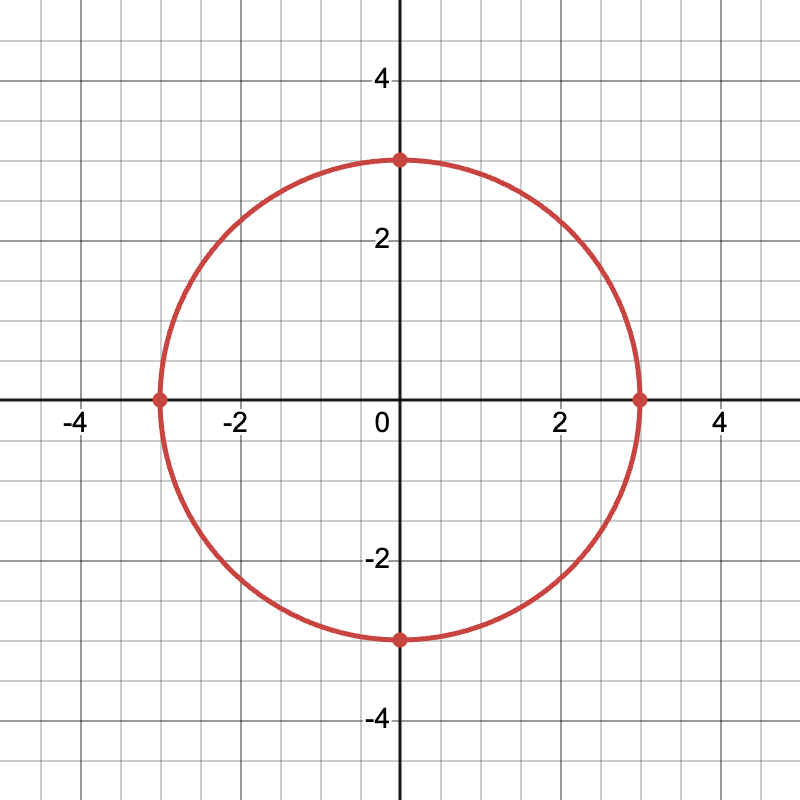
Example 3: Graph a circle with radius 3. The equations are ( x(t) = 3 \cos(t) ), ( y(t) = 3 \sin(t) ), running ( 0 \leq t \leq 2\pi ).
- The complete path forms a circle centered at the origin.
Using Parametric Equations in Real-World Applications
Parametric equations often model real-life scenarios, such as motion paths.
Example 4: Model a projectile’s path. Suppose ( x(t) = 5t ), ( y(t) = 20t - 5t^2 ).
- Here, ( y(t) ) represents vertical motion influenced by gravity, while ( x(t) ) describes constant horizontal speed.
Quick Reference Chart
| Vocabulary | Definition/Key Feature |
| Parametric Equations | Equations defining x and y in terms of a parameter ( t ) |
| Parameter ( t ) | Independent variable controlling other variables |
| Domain | Range of ( t ) values that determine the graph’s extent |
Conclusion
Mastering the graphs of parametric equations in Precalculus opens up many ways to visualize motion and trajectories. This understanding is vital for real-world applications and deeper mathematical exploration. Keep practicing these concepts for a solid foundation and explore more complex scenarios. Happy graphing!
Sharpen Your Skills for AP® Precalculus
Are you preparing for the AP® Precalculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!
Need help preparing for your AP® Precalculus exam?
Albert has hundreds of AP® Precalculus practice questions, free response, and an AP® Precalculus practice test to try out.
