Introduction to the Gravity Model
When discussing urban geography, more particularly cities and urban land use, it is important to understand the gravity model, as we will discuss in this study guide. The gravity model helps to give a clearer understanding of the distribution and size of cities while also providing useful explanations of interactions among networks among cities.
To understand a gravity model definition, you should understand that it is called the gravity model because it is related to Isaac Newton’s Law of Gravitation, which predicts the gravitational force between two objects. Newton’s Law is applied to urban geography in the sense that it determines the strength of the interaction between two urban geographical regions, which can be cities, metropolitan areas, countries, etc. The strength of this interaction can be calculated by the formula below:
S=\dfrac { { P }_{ 1 }{ P }_{ 2 } }{ { D }^{ 2 } }
where { P }_{ 1 } and { P }_{ 2 } are the populations of cities 1 and 2, respectively, D is the distance between the two cities, and S is the interaction strength. The populations are, of course, in units of people, and the distance is generally in units of miles or kilometers, depending upon where in the world you are. The resulting strength is, therefore, in units of { people }^{ 2 }/{ mi }^{ 2 } or { people }^{ 2 }/{ km }^{ 2 }. However, the number is usually just reported without units.
To explain the mathematical relationship, it is the strength of the interaction between two cities (we will assume they are cities for the sake of simplicity for this article, although you should still keep in mind that it could refer to any political or geographical subdivision) is determined by multiplying the population of one city by the population of the second, dividing by the square of the distance between the two cities.
The strength of the interaction between the two cities determines flow between the two cities. Initially, this was used only to account for migration from one place to another. However, the model has been expanded to show that it may explain different types of flow. These various types of flow could be of people, information, commodities, money, labor, and pretty much anything else that moves between two locations. The interaction strength is directly proportional to the population of each city and inversely proportional to the square of the distance. The larger the cities, the stronger the interaction, and the farther the cities are from one another, the weaker the interaction is, with this magnitude being squared. The latter relationship is known as distance decay, which refers to the idea that as distance decreases between two places, so does the interaction in an exponentially decaying manner.
How and why does a fundamental kinematic Newtonian physical equation apply to human geography? When compared to physical objects in Newtonian kinematics, this makes sense because, in that context, the size of each object and distance between objects determines the physical force exerted on one another. In the same way, the size of each city and the distance between them are the primary determinants of how closely the cities are bound together.
Example and Explanation of the Gravity Model

So that you can better see how this works let’s look at an example of two pairs of cities, with one being a pair of the large cities far apart and the other being a pair of smaller cities closer together. In the first pair, we will look at New York City and London, and in the second pair we will look at Amsterdam and Brussels.
As of July 2016, the population of New York City is approximately 8.5 million people and London is 8.2 million people. They are 3,470 miles apart. The population of Amsterdam is approximately 800,000 people and Brussels is 1.2 million people. These two cities are 109 miles apart. Don’t worry, you won’t have to do actual calculations on the AP® exam. This is just to show the implications of the model.
First, let’s calculate the interaction strength between New York City and London, which is 5,788,604. Next, we will do the same for Amsterdam and Brussels, which is 80,801,279.
This shows that although the population of cities determines how important a city is, regarding its push-pull factors and its interaction strength with another city, it is not as strong a factor as the distance is (hence it being squared). Even though New York City and London are two of the largest and most influential cities in the world, while Amsterdam and Brussels are significantly smaller, the fact that Amsterdam and Brussels are much closer to one another than New York City and London has created an interaction strength that is approximately 32 times stronger.
While the gravity model gives a good understanding of the relationship between the two cities and how easily flow occurs between them, there are several weaknesses to the model. The first is that people argue whether, for the distance term, to use the actual geographic distance between two places or to use what is known as the functional distance, which refers to the distance by way of roads, rail, or flights. However, if accounting for overall flow and interaction strength, the functional distance for each measurement would be different. For example, between New York and London, the functional distances would be different for people flying, as opposed to information transmittance, which requires integrating the distance to satellites.
Another criticism of the gravity model relates to the fact that the interaction strength isn’t represented in units. This is because the units resulting from this calculation are physically meaningless while, in the Newtonian gravity model, a gravitational constant is included to give the calculation physical meaning. Therefore, the criticism argues that it is not scientifically verifiable and can only be based on observation.
Also, it makes a sweeping assumption that we know not to be true. It assumes that distance is included in the model regardless of political and physical geography. Obviously, there will be different boundaries that need to be crossed in this regard.
Looking at political geography, let’s take a city like Houston and compare it with Mexico City and New York City. Mexico City has a population of approximately 9 million people within the city limits, slightly higher than that of New York. For the sake of comparison, let us assume that the difference is negligible. However, New York City is approximately twice as far from Houston as Mexico City. This means that flow is nearly four times more likely to occur between Houston and Mexico City than between Houston and New York City. We know that’s not true for several reasons. The main reason is that to get to Mexico City from Houston, we need to cross political boundaries, something we don’t need to do if traveling to New York City. Also, conditions are far worse in Mexico City due to political climate, than in New York City, making flow less likely in this situation.
We can apply the same example to physical geography in that there could be a physical feature that acts as a hindrance, such as mountains or rough physical terrain.
Although there are plenty of ways in which the gravity model can be improved and adjusted to provide a more realistic picture of flow, it still does an excellent job giving an overall picture of how flow occurs between two points. The gravity model has been used for years and will continue to be used to understand how and why flow occurs between certain areas and to what magnitude.
The Gravity Model and the AP® Human Geography Exam
On the AP® Human Geography course description, the idea of the gravity model falls under the category of “Cities and Urban Land Use.” More specifically, you would be asked to use the gravity model to study systems of cities, while focusing on the location of cities, and why cities are where they are. You most likely will not be asked specifically what the gravity model is but rather you will be asked how you can apply it to certain scenarios.
On the AP® Human Geography multiple choice part of the exam, it would be difficult to incorporate the gravity model without it being a straight gravity model definition question. Therefore, you’re far more likely to use it in the free-response question (FRQ) section than in the AP® Human Geography multiple choice section. You would use it on the AP® Human Geography FRQ as a tool to explain a phenomenon that the question is asking.
To help you apply this study guide to the exam as best as possible, here is an example of an AP® Human Geography FRQ from the 2008 AP® Human Geography Exam (Question 2):
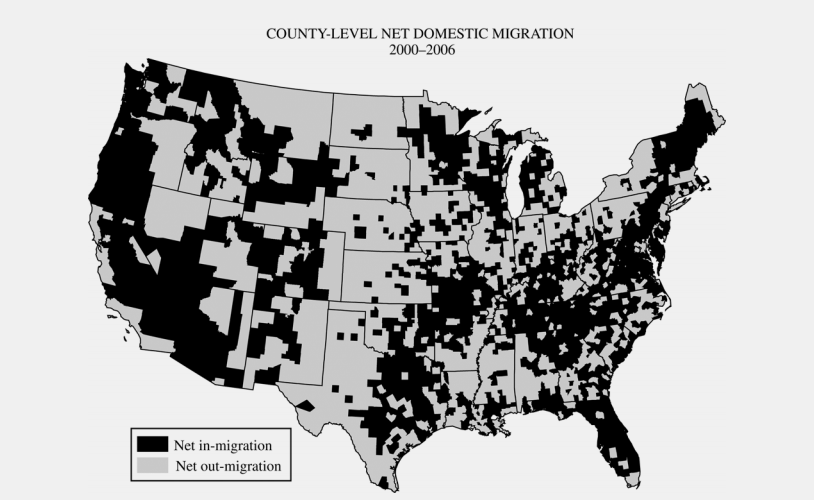
Regional migration patterns within the contiguous United States are the result of several factors. The map above shows net migration at the county level, but these data support generalizations about migration patterns at the regional scale.
A. Identify two specific regions that have experienced net in-migration.
B. Identify two specific regions that have experienced net out-migration.
C. Explain the processes that contribute to the general patterns of migration within the United States shown on the map in terms of each of the following:
1. Economic structure
2. Friction of distance
3. Age structure of the population
You would use the gravity model in part C of this question while addressing the friction of distance. Here, you would say that areas of in-migration are directly related to the gravity model because there is a high amount of interaction between the places. Therefore, people begin to migrate there due to the fact that the magnitude of interaction is higher.
Wrapping up the Gravity Model
To wrap up this section of the study guide, the gravity model definition derives itself from Newton’s Law of Gravitation, and essentially takes two cities and determines the strength of interaction between them by using their populations and distances. The higher the populations, the stronger the interaction, and the farther away the cities are, the lower the interaction is squared, due to the idea of distance decay. Although this model is a good indicator of interaction, some weaknesses mostly pertain to its inability to account for certain variables. You would most likely be asked to use this on the AP® Human Geography FRQ section as a tool to explain certain phenomena related to migration patterns. It is unlikely that you will be asked about this on the AP® Human Geography multiple choice portion of the exam.
How else are you studying for the AP® Human Geography Exam? Let us hear your suggestions!
Looking for AP® Human Geography practice?
Check out our other articles on AP Human Geography.
You can also find thousands of practice questions on Albert.io. Albert.io lets you customize your learning experience to target practice where you need the most help. We’ll give you challenging practice questions to help you achieve mastery in AP® Human Geography.
Start practicing here.
Are you a teacher or administrator interested in boosting AP® Human Geography student outcomes?
Learn more about our school licenses here.








