In vector calculus, the cross product of two vectors is a special operation that gives a new vector perpendicular to both initial vectors. The cross product has many applications in multivariable calculus and computational geometry. In this review article, we’ll define the cross product and investigate its properties. You’ll learn how to calculate the cross product, how to derive the cross product formula, and how to make use of the cross product formula in different applications.
The Cross Product of Two Vectors
For the description of vectors in three-dimensional space, we’ll use the standard orthonormal basis in a right-hand coordinate system, which is formed by vectors \vec{i} , \vec{j} , and \vec{k} . Here, \vec{i} = (1,0,0) is a unit vector along the x-axis, \vec{j} = (0,1,0) is a unit vector along the y-axis, and \vec{k} = (0,0,1) is a unit vector along the z-axis. Any vector \vec{a} = (a_x, a_y, a_z) in three dimensions can be expressed uniquely as the linear combination of vectors \vec{i} , \vec{j} , and \vec{k} in the following way:
\vec{a} = a_x \vec{i} + a_y \vec{j} + a_z \vec{k}
The following image illustrates the decomposition of the vector \vec{a} into the standard basis vectors:
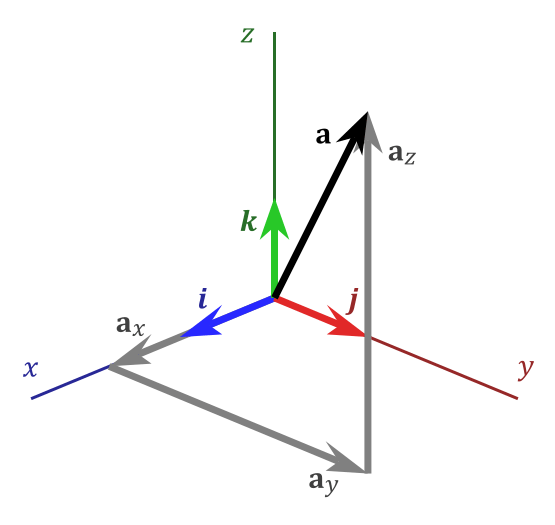
Given two arbitrary vectors \vec{a} = (a_x, a_y, a_z) and \vec{b} = (b_x, b_y, b_z) in space, the cross product \vec{c} = \vec{a} \times \vec{b} is a new vector, \vec{c} = (c_x, c_y, c_z) , such that
\begin{array}{c} c_x = a_y b_z - a_z b_y c_y = a_z b_x - a_x b_z c_z = a_x b_y - a_y b_x \end{array}
This definition can be remembered by writing the cross product as a determinant:
\vec{c} = \vec{a} \times \vec{b} = \det \left|\begin{array}{ccc} \vec{i} & \vec{j} & \vec{k} a_x & a_y & a_z b_x & b_y & b_z \end{array} \right| = (a_y b_z - a_z b_y) \vec{i} + (a_z b_x - a_x b_z) \vec{j} + (a_x b_y - a_y b_x) \vec{k}
The following example illustrates this definition.
Example 1
Let \vec{a} = (1,-3,1) and \vec{b} = (-1,-1,1) . The cross product of the two vectors \vec{a} and \vec{b} in this case is a new vector, \vec{c}, which can be calculated in the following way:
\vec{c} = \vec{a} \times \vec{b} = \det \left|\begin{array}{ccc} \vec{i} & \vec{j} & \vec{k} 1 & -3 & 1 -1 & -1 & 1 \end{array} \right| = (-3+1) \vec{i} + (-1-1) \vec{j} + (-1-3) \vec{k} = -2 \vec{i} -2 \vec{j} -4 \vec{k}
In component notation, we have \vec{c} = \vec{a} \times \vec{b} = (-2,-2,-4).
Cross Product Formula
For two vectors, \vec{a} and \vec{b} , it is convenient to choose a coordinate system such that both vectors lie in thex-y plane, and the x-axis is parallel to vector \vec{a} . In this case, we have \vec{a} = (|\vec{a}|,0,0) and \vec{b} =(|\vec{b}| cos\theta,|\vec{b}| sin\theta,0) , where |\vec{a}| and |\vec{b}| are norms of the vectors \vec{a} and \vec{b} , respectively, and \theta is the angle between the vectors. According to the definition, the cross product of the vectors \vec{a} and \vec{b} in such a coordinate system is equal to
\vec{a} \times \vec{b} = \det \left|\begin{array}{ccc} \vec{i} & \vec{j} & \vec{k} |\vec{a}| & 0 & 0 |\vec{b}| cos\theta & |\vec{b}| sin\theta & 0 \end{array} \right| = |\vec{a}|,|\vec{b}| sin\theta ,\vec{k}
In component notation, we can write \vec{a} \times \vec{b} =(0,0,|\vec{a}|,|\vec{b}| sin\theta) . This result reveals some important properties of the cross product:
1. The cross product of two vectors, \vec{a} and \vec{b} , is the vector \vec{a} \times \vec{b} , which is perpendicular to both \vec{a} and \vec{b}
2. The cross product \vec{a} \times \vec{b} points in the direction from which the rotation from \vec{a} to \vec{b} (through the smaller of thetwo possible angles) appears to be counter-clockwise
3. Unlike the dot product, the cross product is not a commutative operation, and \vec{b} \times \vec{a} = - ,\vec{a} \times \vec{b} . We can easily verify this property by direct calculation:
\vec{b} \times \vec{a} = \left|\begin{array}{ccc} \vec{i} & \vec{j} & \vec{k} |\vec{b}| cos\theta & |\vec{b}| sin\theta & 0 |\vec{a}| & 0 & 0 \end{array} \right| = - ,|\vec{a}|,|\vec{b}| sin\theta ,\vec{k} = - ,\vec{a} \times \vec{b}
4. If vectors \vec{a} and \vec{b} are parallel (i.e., the angle \theta between them is either 0^{\circ} or 180^{\circ} ), the cross product is the zero vector: \vec{a} \times \vec{b} = \vec{0} = (0,0,0)
5. The magnitude of the cross product of two vectors, | \vec{a} \times \vec{b} | , can be given by the following relation:
| \vec{a} \times \vec{b} | = |\vec{a}|,|\vec{b}| sin\theta
This last equality is known as the cross product formula.The cross product formula implies that the magnitude of the cross product |\vec{a} \times \vec{b}| is equal to the area of the parallelogram that has vectors \vec{a} and \vec{b} as its sides, illustrated in the following image:
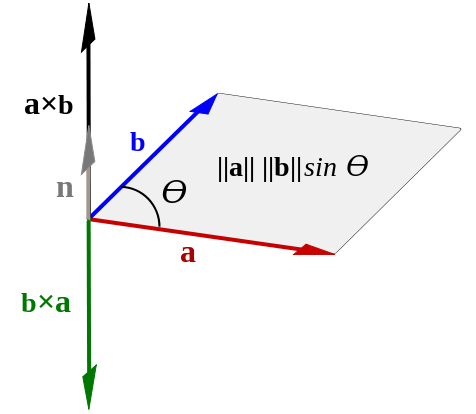
Let’s demonstrate how to use the cross product through examples.
Example 2
Let’s find a vector \vec{c} that is perpendicular to both vectors \vec{a} = (1,1,-1) and \vec{b} = (1,-1,1) . Due to the properties of the cross product, any vector perpendicular to both \vec{a} and \vec{b} is parallel to \vec{a} \times \vec{b} . In other words, \vec{c} = \alpha \left[ \vec{a} \times \vec{b} \right] , where \alpha is some real number. For the cross product of two vectors, \vec{a} and \vec{b} , we have
\vec{a} \times \vec{b} = \det \left|\begin{array}{ccc} \vec{i} & \vec{j} & \vec{k} 1 & 1 & -1 1 & -1 & 1 \end{array} \right| = (1+1) \vec{i} + (-1-1) \vec{j} + (-1-1) \vec{k} = 2 \vec{i} -2 \vec{j} -2 \vec{k}
In component notation, \vec{a} \times \vec{b} = 2(1,-1,-1), and any vector parallel to (1,-1,-1) is perpendicular to both \vec{a} and \vec{b} . We can write \vec{c} = \alpha (1,-1,-1), where \alpha can be any nonzero real number.
Example 3
Consider a parallelogram in the x-y plane. Suppose that the coordinates of the vertices of the parallelogram are B = (0,0) , C = (a,c) , A = (b,d) , and D = (a+b,c+d) , which is illustrated in the following image:

To find the area of this parallelogram, we note that the sides of the parallelogram are vectors in three-dimensional space; namely, \vec{x} = \vec{BC} = (a,c,0) and \vec{x}^{,\prime} = \vec{BA} = (b,d,0) . Then, we can find the cross product of the two vectors, \vec{x} and \vec{x}^{,\prime} :
\vec{x} \times \vec{x}^{,\prime} = \det \left|\begin{array}{ccc} \vec{i} & \vec{j} & \vec{k} a & c & 0 b & d & 0 \end{array} \right| = (ad-bc) ,\vec{k}
Due to the cross product formula, the area of the parallelogram is the norm of the vector \vec{x} \times \vec{x}^{,\prime} , which can be easily calculated:
S = |\vec{x} \times \vec{x}^{,\prime}| = ad-bc
Scalar Triple Product and the Volume of a Parallelepiped
The cross product formula has many applications in computational geometry. For example, it can be used to calculate the volume of a parallelepiped. Let’s see how this can be done. Consider three vectors, \vec{a} , \vec{b} , and \vec{c} , representing three edges of the parallelepiped that meet at one vertex, as illustrated in the image below:

The volume of the parallelepiped, V , can be calculated in the following way:
V = S \cdot h
Here, S is the area of the base, and h is the height of this parallelepiped. The area of the base, due to the cross product formula, is given by the following relation:
S = |\vec{b} \times \vec{c}|
The height of the parallelepiped equals the projection of the vector \vec{a} onto the direction of \vec{b} \times \vec{c} . Thus, we have
h = |\vec{a}| \cdot | cos\phi |
Here, we write the absolute value | cos\phi | to take into account the possibility that the angle \phi is larger than 90^{\circ} . Now, we can use the definition of a dot product of two vectors:
\vec{m} \cdot \vec{n} = m_x n_x + m_y n_y + m_z n_z = |\vec{m}| |\vec{n}| cos\phi
Here, the angle \phi is the angle between the vectors \vec{m} and \vec{n} . Hence, we can write
V = S \cdot h = |\vec{b} \times \vec{c}| \cdot |\vec{a}| \cdot | cos\phi | = | (\vec{b} \times \vec{c},)\cdot \vec{a} |
The dot product of a vector with the cross product of the other two vectors is known as the scalar triple product. Using the definitions of the cross product and dot product, we can derive the following expression:
(\vec{b} \times \vec{c},)\cdot \vec{a} = (b_y c_z - b_z c_y) a_x + (b_z c_x - b_x c_z) a_y + (b_x c_y - b_y c_x) a_z = \det \left|\begin{array}{ccc} a_x & a_y & a_z b_x & b_y & b_z c_x & c_y & c_z \end{array} \right|
It follows from a familiar property of determinants that the scalar triple product is invariant under cyclic permutations of the vectors \vec{a} , \vec{b} and \vec{c} :
(\vec{b} \times \vec{c})\cdot \vec{a} = (\vec{c} \times \vec{a})\cdot \vec{b} = (\vec{a} \times \vec{b})\cdot \vec{c}
Moreover, the scalar triple product vanishes if any two of the vectors \vec{a} , \vec{b} , and \vec{c} are parallel. Naturally, the volume of a parallelepiped is equal to zero in this case. It follows that three vectors are linearly dependent if and only if their scalar triple product vanishes:
(\vec{a} \times \vec{b})\cdot \vec{c} = \det \left|\begin{array}{ccc} a_x & a_y & a_z b_x & b_y & b_z c_x & c_y & c_z \end{array} \right| = 0
If (\vec{a} \times \vec{b})\cdot \vec{c} > 0 , the three vectors \vec{a} , \vec{b} , and \vec{c} form a right-handed basis in space. The basis is left-handed in the opposite case, where (\vec{a} \times \vec{b})\cdot \vec{c} < 0 . A typical right-handed basis consists of the three vectors \vec{i} , \vec{j} , and \vec{k} . This can be demonstrated by direct calculation:
\vec{i} \times \vec{j} = \det \left|\begin{array}{ccc} \vec{i} & \vec{j} & \vec{k} 1 & 0 & 0 0 & 1 & 0 \end{array} \right| = \vec{k} ,, \quad (\vec{i} \times \vec{j})\cdot \vec{k} = \vec{k} \cdot \vec{k} = 1
The following example illustrates how the scalar triple product can be used.
Example 4
Suppose we are given three vectors: \vec{a} = (1,2,3) , \vec{b} = (4,5,0) , and \vec{c} = (3,2,1) . Let’s calculate the scalar triple product of these three vectors:
(\vec{a} \times \vec{b},)\cdot \vec{c} = \det \left|\begin{array}{ccc} 1 & 2 & 3 4 & 5 & 0 3 & 2 & 1 \end{array} \right| = (5-0) + 2(0-4) + 3(8-15) = -,24
Since (\vec{a} \times \vec{b},)\cdot \vec{c} < 0 , the three vectors \vec{a} , \vec{b} , and \vec{c} are linearly independent and form a left-handed basis. The volume of the parallelepiped spanned by the vectors \vec{a} , \vec{b} , and \vec{c} is given by the following expression:
V = |(\vec{a} \times \vec{b},)\cdot \vec{c},| = 24
The Cross Product and Curl of a Vector Field
The cross product plays an important role in multivariable calculus. Consider a vector field \vec{v}(\vec{r},) = {v_x(x,y,z), v_y(x,y,z), v_z(x,y,z)} . The vector field \vec{v} defined in this way, has an important differential characteristic; namely, the curl of \vec{v} , denoted by curl \vec{v} . By definition, the curl of \vec{v} is just the cross product of the differential operator \nabla={\frac{\partial}{\partial x}, \frac{\partial}{\partial y}, \frac{\partial}{\partial z}} :
\text{curl}, \vec{v} = \nabla \times \vec{v} = \det \left|\begin{array}{ccc} \vec{i} & \vec{j} & \vec{k} \dfrac{\partial}{\partial x} & \dfrac{\partial}{\partial y} & \dfrac{\partial}{\partial z} v_x & v_y & v_z \end{array} \right|
It follows that the components of \text{curl}, \vec{v} are defined in the following way:
\begin{array}{c} v_x = \dfrac{\partial v_z}{\partial y} - \dfrac{\partial v_y}{\partial z} v_y = \dfrac{\partial v_x}{\partial z} - \dfrac{\partial v_z}{\partial x} v_z = \dfrac{\partial v_y}{\partial x} - \dfrac{\partial v_x}{\partial y} \end{array}
Let’s illustrate this method of finding the curl of a vector field through a simple example.
Example 5
Consider a vector field, \vec{v} = (-y,x,0) . The curl of \vec{v} can be calculated in the following way:
\text{curl}, \vec{v} = \nabla \times \vec{v} = \det \left|\begin{array}{ccc} \vec{i} & \vec{j} & \vec{k} \dfrac{\partial}{\partial x} & \dfrac{\partial}{\partial y} & \dfrac{\partial}{\partial z} -y & x & 0 \end{array} \right| = \vec{i} \left(-,\dfrac{\partial x}{\partial z}\right) + \vec{j} \left(-,\dfrac{\partial y}{\partial z}\right) + \vec{k} \left(\dfrac{\partial x}{\partial x} + ,\dfrac{\partial y}{\partial y}\right) = 2 \vec{k}
Consequently, in this case, \text{curl}, \vec{v} is a constant vector: \text{curl}, \vec{v} = (0,0,2) .
Wrapping Up the Cross Product
In this review article, we have investigated the cross product and its properties. Now, you will be able to calculate the cross product of two vectors and the curl of a vector. You will also be able to apply the cross product formula to find the area of a parallelogram and the volume of a parallelepiped. We hope this post gives you greater confidence in your knowledge of the cross product and facilitates your studies of multivariable calculus.
Let’s put everything into practice. Try this Multivariable Calculus practice question:
Looking for more Multivariable Calculus practice?
You can also find thousands of practice questions on Albert.io. Albert.io lets you customize your learning experience to target practice where you need the most help. We’ll give you challenging practice questions to help you achieve mastery in Multivariable Calculus.
Start practicing here.
Are you a teacher or administrator interested in boosting Multivariable Calculus student outcomes?
Learn more about our school licenses here.








