Chemical kinetics is the study of how fast reactions go. Chemical reactions occur at different rates. Reaction rate is affected by various variables, such as the nature of reactants, surface area available for the reaction, temperature at which the reaction occurs, concentration of reactants, and catalysts present in the reaction. Some chemical reactions can occur at infinitely slow speed, like geological processes, while others occur rapidly, like nuclear reactions.

Factors Affecting Reaction Rate

Nature of Reactants and Surface Area

Reactions occur because reactants come in contact with each other. The more often reactant molecules collide with each other, the faster the reaction occurs. In order for a reaction to occur effectively, reactant molecules must be moving with sufficient energy, and they must collide in the proper orientation. Reactions involving gaseous reactants occur faster compared to liquid or solid reactants. Having aqueous reactants also affects the reaction rate. They tend to react faster compared to other phases. In a rate law, only gaseous and aqueous reactants are considered. The greater contact area available for the reaction, the faster the reaction occurs. For solid reactants, increasing the surface area by dividing the reactants in smaller sizes will generally increase the rate of reaction.

Temperature

Temperature is the measure of the kinetic energy of a substance. The higher the temperature of a reaction, the more collisions occur. As mentioned earlier, a reaction requires sufficient energy to occur. The minimum energy required to initiate a reaction is called the activation energy. The kinetic energy of the molecules must be higher or equal to the activation energy to create an effective collision. Generally, the higher the temperature, the faster the reaction occurs. Svante Arrhenius formulated an equation that shows the relationship between temperature and activation energy. Arrhenius’ equation shows the dependence of rate constant to temperature:

k=Ae^{-\dfrac{E_a}{RT}}

…where k = rate constant, A = pre-exponential factor, R = gas law constant, T = temperature, and E_a = activation energy.

Arrhenius’ equation shows that with a higher temperature and lower activation energy, the rate constant has a higher value. Larger rate constants favor faster reactions.

Catalyst

Catalysts are substances added in the reaction, but that do not participate in the reaction. Catalysts are used to lower the activation energy of a reaction. This provides an alternate route with a lower activation energy, speeding up the process. When a reaction is finished, the amount of catalyst will still be the same, as they are not consumed in the reaction.

Concentration of Reactants

Reaction rates are usually expressed in terms of the concentration of reactants consumed or the amount of products formed in a given unit of time. Generally, the reaction rate is directly proportional to the concentration of reactants. Having more reactants increases the chance of collision between the reactants. The higher the reactant concentration, the faster the reaction goes.

Rate Laws

A rate law represents the relationship between the rate of the reaction and concentration of reactants. The rate law is a mathematical expression based on experimental data and can be used to predict the behavior of the reaction. We will discuss how to find rate laws for chemical reactions.

In the general reaction:

aA+bB\rightarrow cC+dD

…the rate law can be expressed as:

\text{Rate}=k\left[ A \right]^x \times \left[ B \right]^y

…where k is the proportionality constant in the equation called the rate constant. The value of k mainly depends on the temperature at which the reaction occurs. [A] and [B] are the concentration of the reactant at any moment of the reaction. x and y are the orders of the reaction based on the specific reactant. It indicates the extent to which a certain reactant affects the reaction. The overall order of reaction is the sum of x and y. There are reactions wherein the order is equal to the coefficient of the reactant in the balanced reaction. This type of reaction is called an elementary reaction. That is, in an elementary reaction, x=a and y=b.

Differential and Integrated Rate Laws

The differential rate law expresses the rate of reaction as a function of the rate of disappearance of reactants or the rate of product formation over a certain period of time. Differential rate law helps us picture out the mechanism of reaction. For a general reaction, aA+bB\rightarrow cC+dD, the differential rate law will be:

\text{Rate}=-\dfrac{1}{a} \times \dfrac{\Delta [A]}{\Delta t} =-\dfrac{1}{b} \times \dfrac{\Delta [B]}{\Delta t}=\dfrac{1}{c} \times \dfrac{\Delta [C]}{\Delta t}=\dfrac{1}{d} \times \dfrac{\Delta [D]}{\Delta t}

The negative sign signifies that the species is consumed in the reaction and acts as reactant.

In a differential rate law, it is easier to compare the rate of disappearance and rate of formation of species in the reaction. The differential rate law is useful in finding the instantaneous rate of reaction, the change in concentration of a species over an infinitely small time interval. The instantaneous rate is equal to the slope in the graph of concentration of species vs. time.

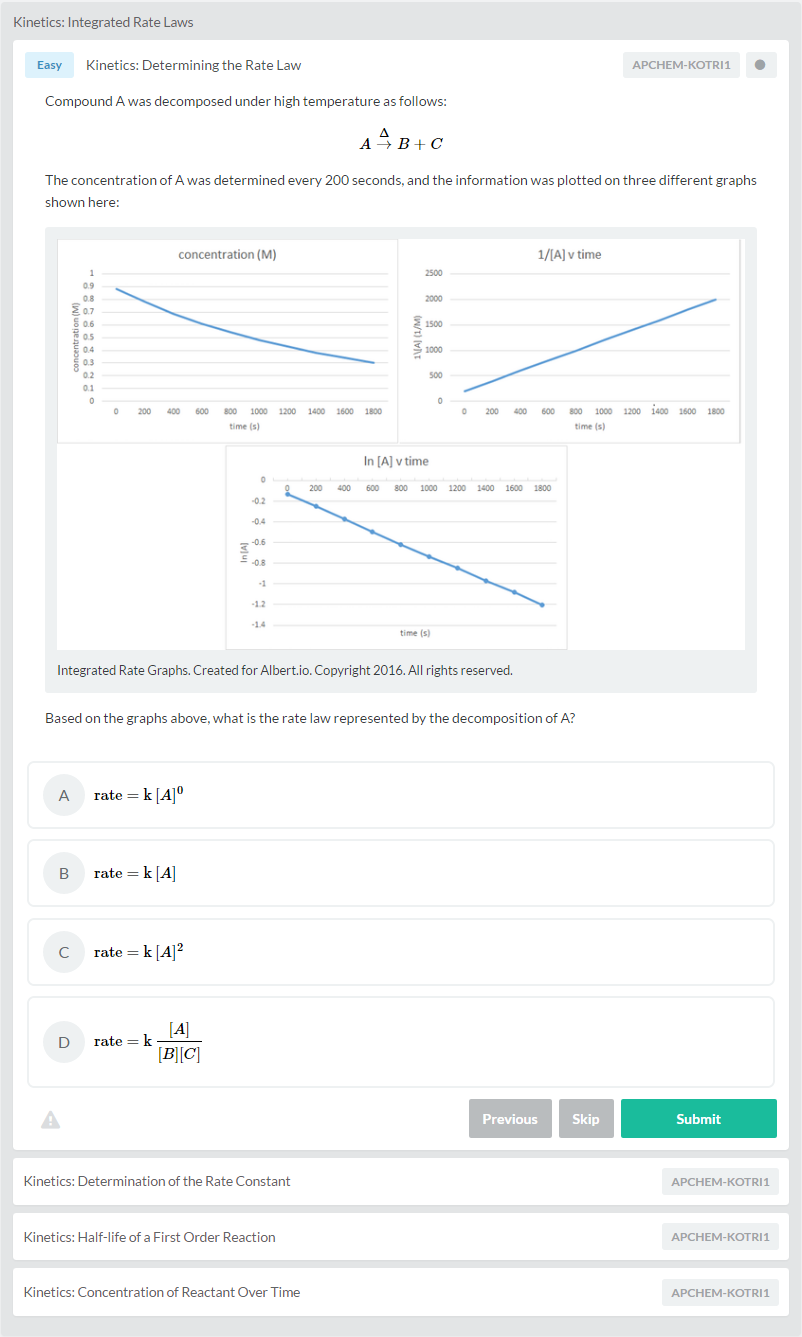
We have the graph below. In order to find the instantaneous rate of reaction, we need to pick two points on the curve.

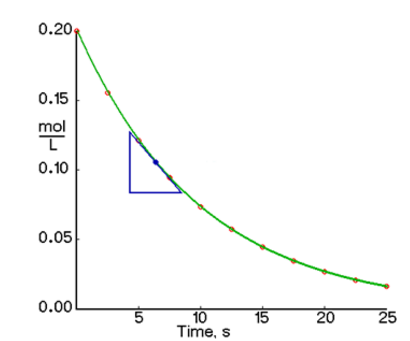
To solve for the instantaneous rate, which is equal to the slope, we have:

{ t }_{ 1 }= 7 \text{ seconds}, { \left[ A \right] }_{ 1 }= 0.11\text{ mol/L}

{ t }_{ 2 }= 8 \text{ seconds}, { \left[ A \right] }_{ 2 }= 0.09\text{ mol/L}

-\dfrac{\Delta [A]}{\Delta t}=-\dfrac{[A]_2-[A]_1}{t_2-t_1}

-\dfrac{0.09 \text{ mol/L} - 0.11 \text{ mol/L}}{8 \text{ s} - 7 \text{ s}}

0.02 \dfrac{\text{mol}}{\text{L} \cdot \text{s}}

While the differential rate law gives you an overview of the reactant disappearance and product formation rates, the integrated rate law is useful in estimating the amount of reactant left after a specific period of time.

The integrated rate law is a function of the initial concentration of a specific reactant and relates concentration with time in an equation. The integrated rate law lets us know how much time is needed to consume a specified amount of reactant, how much reactant remains after a given period of time, and the initial amount of the reactant. The integrated rate law of a reaction depends on the overall order of the reaction.

First Order Reaction

First order reactions are reactions with a linear relationship between reaction rate and reactant concentration. The general form of a first order reaction is:

A \rightarrow \text{products}

For this reaction, the rate law is:

\text{Rate} =-\dfrac{d[A]}{dt} = k[A]

Integrating this rate law expression will give us the integrated rate law for a first order reaction.

-\dfrac{d[A]}{dt} = k[A]

Setting { \left[ A \right] }_{ 0 } as the initial concentration and [A] as final concentration at given time, t:

\displaystyle \int _{ [A_0] }^{ [A] }{ \dfrac{d[A]}{[A]} } =\int _{0}^{t}{-kdt}

ln \dfrac{[A]}{[A]_0} = -kt

\dfrac{[A]}{[A]_0} = e^{-kt}

[A] =[A]_0 e^{-kt}

The final equation is also known as the general form of a first order reaction. We can use it to find the amount of reactant remaining after a given period of time.

The rate equation can also be written as ln { \left[ A \right] } =-kt+ln { \left[ A \right] }_0, which can be compared to slope-intercept form of line equation, y=mx+b. In this form, we can see that if the reaction is a first order, it will form a line in the graph of ln { \left[ A \right] } vs time. The slope of the line will be equal to -k.

The half-life is the time at which half of the initial amount of reactant remains in the reaction. This is commonly used to define the decay of a species. For the first order reaction, the half-life is constant, no matter the reactant concentration.

t_{\dfrac{1}{2}} = \dfrac{ln 2}{k}

Sample Problems

1. Calculate the half-life of a first order reaction given that 37\% of the original amount of the substance has been consumed after 56 \text{ seconds}.

Solution:

Since 37\% of the original amount is consumed, then the remaining amount of the reactant is equal to:

100\% - 37\% = 63\%

Using the general equation for the first order reaction:

ln \dfrac{[A]}{[A]_0} = -kt

ln \dfrac{0.63}{1} = -k (56 \text{ s})

\dfrac{-0.462}{56 \text{ s}} = k

k=0.0083 \text{ s}^{-1}

Now that we have the value of the rate constant, we can now solve for the value of half-life using the formula for a first order reaction.

t_{\dfrac{1}{2}} = \dfrac{ln 2}{k}

t_{\dfrac{1}{2}} = \dfrac{ln 2}{0.0083 \text{ s}^{-1}}

t_{\dfrac{1}{2}} = 83.52 \text{ s}

2. The decomposition of aqueous hydrogen peroxide is a first-order reaction. If it takes 6.5 \text{ hours} for the concentration of H_2O_2 to decrease from 0.70 to 0.35, how many hours are required for the concentration to decrease from 0.40 to 0.10?

Solution:

For this problem, we need to get the value of the rate constant first using the first conditions given.

Condition 1:

t = 6.5 \text{ hours}

{ \left[ A \right] }_{ 0 }= 0.70

[A] = 0.35

ln \dfrac{[A]}{[A]_0} = -kt

ln \dfrac{0.35}{0.70} = -k(6.5 \text{ hr})

\dfrac{-0.693}{6.5 \text{ hr}} = k

k = 0.1066 \text{ hr}^{-1}

Now, solving for the time for the concentration to decrease from 0.40 to 0.10:

ln \dfrac{[A]}{[A]_0} = -kt

ln \dfrac{0.10}{0.40} = -0.1066 \text{ hr}^{-1}(t)

\dfrac{-1.3863}{-0.1066}\text{ hr}= t

t =13\text{ hr}

A simple way of solving this type of problem is by using the concept of half-life. We can see that from concentration 0.70 to 0.35, one half-life of a substance has passed. This means that the half-life of the given reaction is 6.5 text{ hours}. Now, having a concentration of 0.40 decreased to 0.10, we have a total of two half lives passed. This means that to decrease the concentration in that form, a total of 13 text{ hours} is needed.

Second Order Reaction

A second order reaction has reaction rates proportional to the square of reactant concentration. The general form for a second order reaction is:

2A \rightarrow \text{products}

Another reaction that falls into the second order is the reaction of two reactants, both of which have equal concentration at the start of reaction. The general form of two-reactant second order reaction is:

A+B \rightarrow \text{products}

For this type of reaction, the rate law is given as:

\text{Rate} =-\dfrac{d[A]}{dt} = k[A]^2 = k[A][B]

Integrating this rate law expression will give us the integrated rate law for a first order reaction:

-\dfrac{d[A]}{dt} = k[A]^2

Setting { \left[ A \right] }_{ 0 } as the initial concentration and [A] as final concentration at given time, t:

\displaystyle \int _{ [A_0] }^{ [A] }{ \dfrac{d[A]}{[A]^2} } =\int _{0}^{t}{kdt}

\dfrac{1}{[A]}-\dfrac{1}{[A]_0} = kt

\dfrac{1}{[A]}=\dfrac{1}{[A]_0} + kt

As we can see from the equation, the graph of a second order reaction that will form a line is \dfrac{1}{[A]} vs. time. This graph will have a slope of k.

Second order reaction has a half-life that depends on the initial concentration of the reactant. The formula below is used to solve for the half-life of the reaction.

t_{\dfrac{1}{2}} = \dfrac{1}{k[A]_0}

Zero Order Reaction

A special kind of reaction with a rate that is independent of the reactant concentration is called the zero order reaction. As the name implies, the overall order of the reaction is zero, which means that the sum of all exponents in the rate law is zero.

\text{Rate} =-\dfrac{d[A]}{dt} = k

Integrating this rate law expression will give us the integrated rate law for a first order reaction.

-\dfrac{d[A]}{dt} = k

Setting { \left[ A \right] }_{ 0 } as the initial concentration and [A] as final concentration at given time, t:

\displaystyle \int _{ [A_0] }^{ [A] }{ d[A] } =\int _{0}^{t}{-kdt }

[A]-[A]_0 = -kt

[A]=[A]_0 - kt

The linear graph of a zero order reaction is shown in the plot of concentration vs. time. We can see that the rate of reaction is constant over time.

The half-life for a zero order reaction is solved using the formula below:

t_{\dfrac{1}{2}} = \dfrac{[A]_0}{2k}

The table below shows the summary of the order of reactions and can be handy in your AP® Chemistry review.

Another way of finding the rate law of a reaction is using the method of initial rates. In this method, we are given the experimental data, which is comprised of different initial rates run at several trials. The order of the reaction and the rate constant are unknown.

Let’s consider the reaction of acetone and bromide. The following data is collected over three trials.

The general form for the rate law of this reaction is:

Rate=k\left[ { C }_{ 3 }{ H }_{ 6 }O \right] \times \left[ { Br }_{ 2 } \right]^{ y }

Using ratio and proportion:

\dfrac{\text{Rate } 1}{\text{Rate } 2} = \dfrac{k[C_3H_6O]^x[Br_2]^y}{k[C_3H_6O]^x[Br_2]^y}

\dfrac{1.64 \times 10^{-5}}{1.65 \times 10^{-5}} = \dfrac{k[0.25]^x[0.25]^y}{k[0.25]^x[0.50]^y}

1 = \dfrac{[0.25]^y}{[0.50]^y}

0.50^y = 1

y = 0

Now, using Rates 1 and 3:

\dfrac{\text{Rate } 1}{\text{Rate } 3} = \dfrac{k[C_3H_6O]^x[Br_2]^y}{k[C_3H_6O]^x[Br_2]^y}

\dfrac{1.64 \times 10^{-5}}{3.29 \times 10^{-5}} = \dfrac{k[0.25]^x[0.25]^y}{k[0.50]^x[0.25]^y}

0.498 =\dfrac{[0.25]^x}{[0.50]^x}

0.50^x = 0.498

x = 1

We are not yet finished with the solution because we still need to find the value of the rate constant. Using the conditions of the first trial, we have:

\text{Rate} =k[C_3H_6O]^x[Br_2]^y

1.64 \times 10^{-5} = k(0.25)^1(0.25)^0

k = 6.56 \times 10^{-5}

Now, the general rate law for the bromination of acetone is:

\text{Rate} =6.56 \times 10^{-5}[C_3H_6O]

To find the rate laws for AP® Chemistry, you can use the order of reaction method or the method of initial rate.

Let’s put everything into practice. Try this AP® Chemistry practice question:

Looking for more AP® Chemistry practice?

Check out our other articles on AP® Chemistry.

You can also find thousands of practice questions on Albert.io. Albert.io lets you customize your learning experience to target practice where you need the most help. We’ll give you challenging practice questions to help you achieve mastery of AP® Chemistry.

Start practicing here.

Are you a teacher or administrator interested in boosting AP® Chemistry student outcomes?

Learn more about our school licenses here