We are confident you have come across the term trapezoid rule in class or read about it in books. Have you ever wondered how it’s use? How to answer questions that require the use of the trapezoid rule and how the trapezoid rule is applied to tackle such questions? We will explain these in detail and make problems that require the trapezoid rule as easy as one plus one.
The trapezoid rule is used to approximate the area under a graph or to estimate the value of an integral. Let’s now go into detail to see its derivation and how it is applied.
Consider the two graphs shown below:
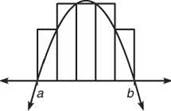
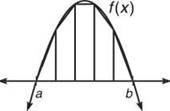
Image Source: SchoolBag
Notice that in the first graph; there is lots of extra space in the rectangles as compared to the second graph that contains trapezoids. Thus, we can have a better approximation of the area under the curve by using trapezoids subdivisions.
Now recall that the area of a trapezoid is given by:
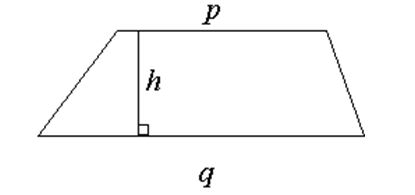
Area=\dfrac{h}{2}(p+q)
where h is the height of the trapezoid and p and q are the lengths of its two parallel sides.
To find the area under the graph we will simply add the area of the trapezoids.
The approximate area under the curve is:
Area=\dfrac{1}{2}\left({y}_{0}+{y}_{1}\right)\Delta x+\dfrac{1}{2}\left({y}_{1}+{y}_{2}\right)\Delta x+\dfrac{1}{2}\left({y}_{2}+{y}_{3}\right)\Delta x+...
Let us now jump into the trapezoid rule itself. How it is written and how we apply it.
The Trapezoid Rule
If a function f, is continuous on the closed interval [a, b] divided into n equal intervals, then the area between the curve and x-axis is approximated to be:
Area \approx \dfrac{h}{2} \sum_{i=1}^{n}{\left[f\left({x}_{i+1}\right)+f\left({x}_{i}\right)\right]}
Where the height h, corresponds to the width ∆x. That is:
h=\Delta x=\dfrac{b-a}{n}
The trapezoid rule is given by:
Area \approx \dfrac {\Delta x}{2} \sum_{i=1}^{n}{\left[f\left({x}_{i+1}\right)+f\left({x}_{i}\right)\right]}
When expanded and simplified, the trapezoid rule is:
Area \approx \dfrac {\Delta x}{2} \left[f \left(a \right)+2f \left({x}_{1} \right)+2f \left({x}_{2} \right)+2f \left({x}_{3} \right)+...+2f \left({x}_{n-1} \right)+f \left(b \right) \right]
The use of the trapezoid rule does not change when estimating the value of an integral; we just substitute the integral in place of the area:
\int_{a}^{b}{f \left(x \right)dx \approx \dfrac {\Delta x}{2} \left[f \left({x}_{0} \right)+2f \left({x}_{1} \right)+2f \left({x}_{2} \right)+2f \left({x}_{3} \right)+...+2f \left({x}_{n-1} \right)+f \left({x}_{n} \right) \right]}
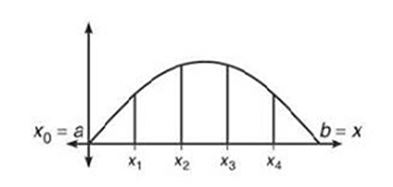
To approximate the area, we find the width ∆x, divide it by two then multiply it by the sum of the functions doubled except the first and the last function.
The middle f\left({x}_{i}\right) are multiplied by two since they represents the parallel sides shared by two adjacent trapezoids.
Now let us look at some examples to see how the trapezoid rule is used for approximation.
Example 1
Using n=5, approximate the integral; \int_{0}^{1}{\sqrt{{2x}^{2}+1}dx}
Solution:
Graphing the function we have:
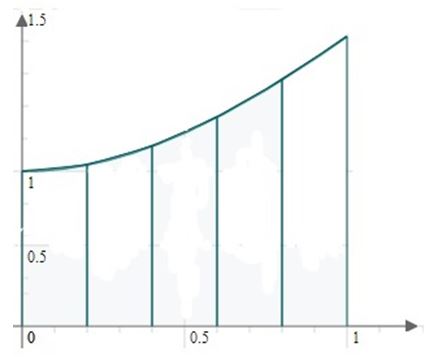
The trapezoid rule states:
\int_{a}^{b}{f\left(x\right)dx \approx \dfrac {\Delta x}{2}\left[f\left({x}_{0}\right)+2f\left({x}_{1}\right)+2f\left({x}_{2}\right)+2f\left({x}_{3}\right)+...+2f\left({x}_{n-1}\right)+f\left({x}_{n}\right)\right]},
where \Delta x=\dfrac{b-a}{n}.
We have that a=0,b=1,n=5.
Therefore,
\Delta x=\dfrac{1-0}{5}.
Divide interval [1, 0] into n=5 subintervals of length \Delta x=\dfrac{1}{5} with the following endpoints:
a=0, \dfrac{1}{5}, \dfrac{2}{5}, \dfrac{3}{5}, \dfrac{4}{5},1=b.
Now, we just evaluate functions at the endpoints:
f\left({x}_{0}\right)=f\left(a\right)=f\left(0\right)=1
2f\left({x}_{1}\right)=2f\left(\dfrac{1}{5}\right)=\dfrac{6\sqrt{3}}{5}=2.07846
2f\left({x}_{2}\right)=2f\left(\dfrac{2}{5}\right)=\dfrac{6\sqrt{33}}{5}=2.29782
2f\left({x}_{3}\right)=2f\left(\dfrac{3}{5}\right)=\dfrac{2\sqrt{43}}{5}=2.62298
2f\left({x}_{4}\right)=2f\left(\dfrac{4}{5}\right)=\dfrac{6\sqrt{57}}{5}=3.01993
f\left({x}_{5}\right)=f\left(b\right)=f\left(1\right)=\sqrt{3}=1.73205
Finally, we just sum up the above values then multiply by \dfrac{\Delta x}{2}=\dfrac{1}{10}.
\dfrac{1}{10}\left(1+2.07846+2.29782+2.62298+3.01993+1.73205\right)=1.2751 \int_{0}^{1}{\sqrt{{2x}^{2}+1}dx}\approx1.2751
Now we will compare our approximation to the exact integral:
\int_{0}^{1}{\sqrt{{2x}^{2}+1}dx}\approx1.27127
That was close, right? You see how easy it is to use the trapezoid rule. Let us try another example then check some past AP® Calculus questions that required us to apply the trapezoid rule.
Example 2
Use trapezoid rule to approximate the area beneath the curve f\left(x\right)={x}^{2}+5 on the interval [0,4] using 4 subintervals.
Solution:
We already know the definition of the trapezoid rule, so that we will just jump into the solution.
We have that a=0,b=4,n=4
Therefore, \Delta x=\dfrac{4-0}{4}=1 .
Divide interval [0,4] into n=4 subintervals of length \Delta x=1 with the following endpoints:
a=0,1,2,3,4=b
Now, we just evaluate functions at those endpoints:
f\left({x}_{0}\right)=f\left(a\right)=f\left(0\right)=5
2f\left({x}_{1}\right)=2f\left(1\right)=12
2f\left({x}_{2}\right)=2f\left(2\right)=18
2f\left({x}_{3}\right)=2f\left(3\right)=28
f\left({x}_{4}\right)=f\left(b\right)=f\left(4\right)=21
The final step is just to sum up the above values and multiply by \dfrac{\Delta x}{2}=\dfrac{1}{2}.
\approx \dfrac{1}{2}\left(5+12+18+28+21\right)
\approx 42
Let us see how close our approximation is by determining the exact integral.
\int_{0}^{4}{{x}^{2}+5}dx \approx 41.333
That was so close to the exact answer, wasn’t it?
Now let us jump into some past years AP® Calculus AB Free Response Questions that required the use of the trapezoid rule for approximating integrals.
2010 AP® Calculus AB FREE RESPONSE QUESTIONS 2(b)
| t (hours) | 0 | 2 | 5 | 7 | 8 |
| E (t) (Hundreds of entries) | 0 | 4 | 13 | 21 | 23 |
A zoo sponsored a one-day contest to name a new baby elephant. Zoo visitors deposited entries in special box between noon (t=0) and 8 P.M(t=8). The number of entries in the box t hours after noon is modeled by a differentiable function E for 0\le t \le8. Values of E(t), in hundreds of entries, at various times are shown in the table above. b) Use a trapezoidal sum with four subintervals given by the table to approximate the value of \dfrac{1}{8}\int_{0}^{8}{E\left(t\right)dt}. Using correct units, explain the meaning of \dfrac{1}{8}\int_{0}^{8}{E\left(t\right)dt} in terms of the number of entries.
Solution:
Since the intervals of t have varying widths, we will work out the area of each trapezoid then sum the areas.
Area of a trapezoid is given by:
Area=\dfrac{h}{2}(p+q)
Where h is the height (in this case width), p and q are the two parallel sides.
\dfrac{1}{8}\int_{0}^{8}{E\left(t\right)dt=\dfrac{1}{8}\left({A}_{1}+{A}_{2}+{A}_{3}+{A}_{4}\right)}
Where {A}_{1},{A}_{2},{A}_{3}, and {A}_{4} are the areas of the 4 subintervals.
Area of {A}_{1} (between t=0 and t=2):
\Delta x=2-0=2; {A}_{1}=\dfrac{1}{2}\times2\left(0+4\right)=4
Area of {A}_{2} (between t=2 and t=5):
\Delta x=5-2=3; {A}_{2}=\dfrac{1}{2}\times3\left(4+13\right)=25.5
Area of {A}_{3} (between t=5 and t=7):
\Delta x=7-5=2; {A}_{3}=\dfrac{1}{2}\times2\left(13+21\right)=34
Area of {A}_{4} (between t=7 and t=8):
\Delta x=8-7=1; {A}_{4}=\dfrac{1}{2}\times1\left(21+23\right)=22
The final step is, to add up, the areas and multiply by \dfrac{1}{8}.
\approx \dfrac{1}{8}\left(4+25.5+34+22\right)
\approx 10.6875
The integral \dfrac{1}{8}\int_{0}^{8}{E\left(t\right)dt} gives the average number of entries, in hundreds, in the box from noon till 8P.M.
Have you just seen how we have tackled it? Seems simple, right? Let us look at another past question.
2011 AP® Calculus AB FREE RESPONSE QUESTIONS 2(b)
| t (minutes) | 0 | 2 | 5 | 9 | 10 |
| H (t) (degree celsius) | 66 | 60 | 52 | 44 | 43 |
b) Using correct units, explain the meaning of \dfrac{1}{10}\int_{0}^{10}{H\left(t\right)dt} in the context of this problem. Use a trapezoidal sum with the four subintervals indicated by the table to estimate \dfrac{1}{10}\int_{0}^{10}{H\left(t\right)dt}. As a pot of tea cools, the temperature of the tea is modeled by a differentiable function H for 0\le t \le 10, where time is measured in minutes and temperature H(t) at selected values of time t are shown in the table above.
Solution:
\dfrac{1}{10}\int_{0}^{10}{H\left(t\right)dt} is the average temperature,
in degrees Celsius, of the cooling tea in the given time interval 0\le t \le 10
Area \approx \dfrac{1}{10}\int_{0}^{10}{H\left(t\right)dt=\dfrac{1}{10}\left({A}_{1}+{A}_{2}+{A}_{3}+{A}_{4}\right)}
Where {A}_{1},{A}_{2},{A}_{3},and {A}_{4} are the areas of the 4 subintervals.
Area of {A}_{1} (between t=0 and t=2):
\Delta x=2-0=2; {A}_{1}=\dfrac{1}{2}\times2\left(66+60\right)=126
Area of Area of {A}_{2} (between t=2 and t=5):
\Delta x=5-2=3; {A}_{2}=\dfrac{1}{2}\times3\left(60+52\right)=168
Area of Area of {A}_{3} (between t=5 and t=9):
\Delta x=9-5=4; {A}_{3}=\dfrac{1}{2}\times4\left(52+44\right)=192
Area of Area of {A}_{4} (between t=9 and t=10):
\Delta x=10-9=1; {A}_{4}=\dfrac{1}{2}\times1\left(44+43\right)=43.5
Final step is to sum up the areas and multiply by \dfrac{1}{10}.
\approx \dfrac{1}{10}\left(126+168+192+43.5\right)
\approx{52.95}^{0}C
Hopefully, you have noticed that nothing changes much in these kinds of questions, and we just use the very same steps to arrive at the answer.
CONCLUSION
Going through the sample questions and solutions I bet you have noticed how the application of the trapezoidal rule is easy to use. After grasping the formula well and knowing how to plug in the numbers, you are good to go.
Recapping on what we have covered today:
1. Trapezoid rule is given by:
\int_{a}^{b}{f\left(x\right)dx \approx \dfrac{\Delta x}{2}\left[f\left({x}_{0}\right)+2f\left({x}_{1}\right)+2f\left({x}_{2}\right)+2f\left({x}_{3}\right)+...+2f\left({x}_{n-1}\right)+f\left({x}_{n}\right)\right]}
Where the width is given by: \Delta x=\dfrac{b-a}{n}
2. Questions that require the use of the trapezoidal rule can be set in two ways.
i. Using the trapezoidal rule to approximate the value of an integral.
ii. Using the trapezoidal rule to approximate the area under a curve.
3. Accuracy is increased by using more trapezoids, that is, increasing the number of n
We know from now on, questions that require the application of the trapezoid rule will be your favorites since they are quite easy to solve.
Let’s put everything into practice. Try this AP® Calculus practice question:
Looking for more AP® Calculus practice?
Check out our other articles on AP® Calculus.
You can also find thousands of practice questions on Albert.io. Albert.io lets you customize your learning experience to target practice where you need the most help. We’ll give you challenging practice questions to help you achieve mastery of AP® Calculus.
Start practicing here.
Are you a teacher or administrator interested in boosting AP® Calculus student outcomes?
Learn more about our school licenses here.









