Acids and Bases Definitions
This AP® Chemistry crash course review will go over the fundamentals of acids and bases in chemistry and their applications to the AP® Chemistry exam. There are three definitions of what constitutes an acid and a base. Each of these definitions is useful for different purposes.
1. Arrhenius Definition: Acids are compounds that increase the concentration of protons \left( { H }^{ + } \right) in an aqueous solution. Bases are compounds that increase the concentration of hydroxide ions \left( { OH }^{ - } \right) in an aqueous solution. When acids and bases react, they undergo a neutralization reaction, and the products are a salt and water.
2. Brønsted-Lowry Definition: Acids are compounds that donate hydrogen atoms \left( { H }^{ + } \right), and bases are compounds that accept hydrogen atoms. Acids donate their hydrogen and become conjugate bases, and bases react with protons to form conjugate acids. Acids and bases that dissociate completely are called strong acids and bases, and those that only partially dissociate are called weak acids and bases and form equilibrium mixtures in solution.
3. Lewis Definition: Acids are compounds that can accept an incoming electron pair, and bases are compounds that donate electron pairs to other compounds.
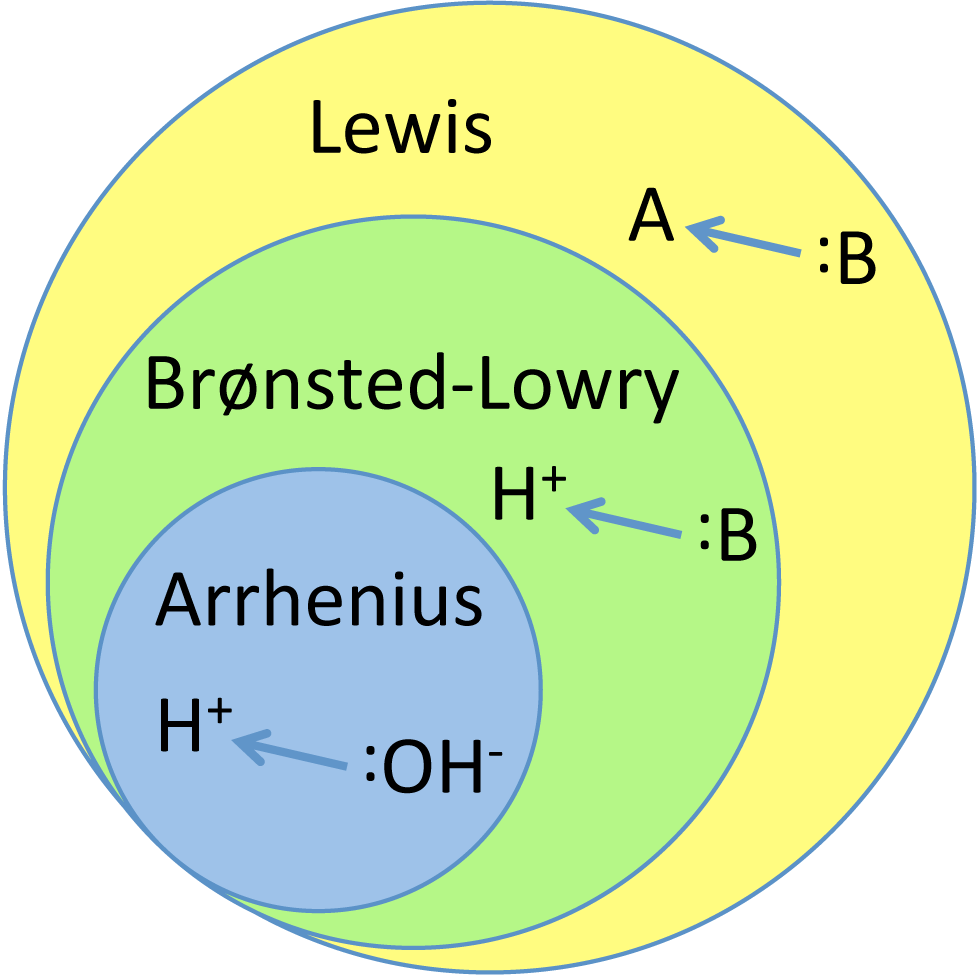
The three definitions of acids or bases are more generalized as we go from top to bottom. The Arrhenius definition only encompasses compounds that increase the concentration of hydrogen ion and hydroxide moieties in an aqueous solution. The Brønsted-Lowry definition encompasses all compounds that are capable of donating hydrogen atoms to one another, regardless of the solvent they reside in; this definition encompasses those compounds that are classified as acids or bases in the Arrhenius definition, such as acetic acid. The Lewis takes away the necessity for hydrogen ions and instead defines acids in bases in terms of electron pairs; this applies to any compounds that are acids and bases under either the Arrhenius or the Brønsted-Lowry definition. The main point to remember is that all three definitions of acids and bases are internally consistent with each other.
The first topic that must be covered in any discussion about acids and bases is how we measure a solutions’ acidity. The acidity of a solution is most commonly measured on the pH scale. The pH of a solution is a measure of the concentrated of hydrogen ions \left( { H }^{ + } \right), or protons) in solution. To be exact, the pH of a solution is the negative log of the concentration of protons in solution.
pH=-log { { [H }^{ + }] }
The pH scale ranges from 0 to 14 for reasons we will discuss below. Before we get there, another useful scale to know is the pOH scale. The pOH of a solution is a measure of the concentration of hydroxide ions \left( { OH }^{ - } \right) in solution, also in the negative log form.
pOH=-log { { [OH }^{ - }] }
The pH and pOH scales are related to each other due to the equilibrium that exists between hydrogen ions and hydroxide in solution. For a given solution, the sum of the pH and pOH of the solution must always equal 14.
pH+pOH=14
To understand why this relationship must be true, we have to review in more detail the term acid and base as defined in the Brønsted-Lowry definition. The Brønsted-Lowry definition considers acids to be any protonated compound capable of donating its protons; these species are represented by the figureAH, where “A” is the fundamental compound and “H” is the donated proton. A base is defined as any species that can accept a donated proton. The deprotonated base is represented by the symbol “B”. When a protonated acid comes in contact with a base, the acid donates the proton to the base, thus protonating the base and itself become deprotonated. This can be represented by the chemical expression below:
AH + B \leftrightarrow A^-+ BH^+
And the equilibrium expression for the reaction would be:
K = \dfrac{ { [AH] }{ [B] } }{ { [A] }^{ - }{ [BH] }^{ + } }
One of the most important consequences of the Brønsted-Lowry definition is that a deprotonated acid can regain its donated proton, and a protonated base can become deprotonated once more. We call the deprotonated acid species the conjugate base because of its ability to function as a proton acceptor (Brønsted-Lowry base). The protonated base then becomes a conjugate acid because of its ability to donate protons. The two species exist in an equilibrium mixture represented by the expression above. The only exceptions to this rule are the seven so-called “strong” acids and eight strong bases whose conjugate acids and bases are so weak that their dissociation in water is not considered to be reversible.
How does this tie into the pH of a solution? Well, in aqueous media, the hydrogen ion is also known as hydronium since in reality protons dissolved in water form weak bonds to the solvent water molecules. This relationship is represented by the molecule known as the hydronium ion, { H }_{ 3 }{ O }^{ + }. The Brønsted-Lowry definition enumerates that water molecules are an amphoteric species, meaning that they can act both as an acid or a base. The reaction that illustrates this is the grabbing of a proton from one water molecule by another water molecule, resulting in the formation of a hydronium { H }_{ 3 }{ O }^{ + } and hydroxide\left( { OH }^{ - } \right) ion:
{ 2H }_{ 2 }O\leftrightarrow { OH }^{ - }+{ H }_{ 3 }{ O }^{ + }
And the reaction is represented by the equilibrium expression below, where w stands for water.
{ K }_{ w }=\left[ { OH }^{ - } \right] \left[ { H }_{ 3 }{ O }^{ + } \right] ={ 1.0 \times 10 }^{ -14 } at 25 ^{\circ} \text{C}
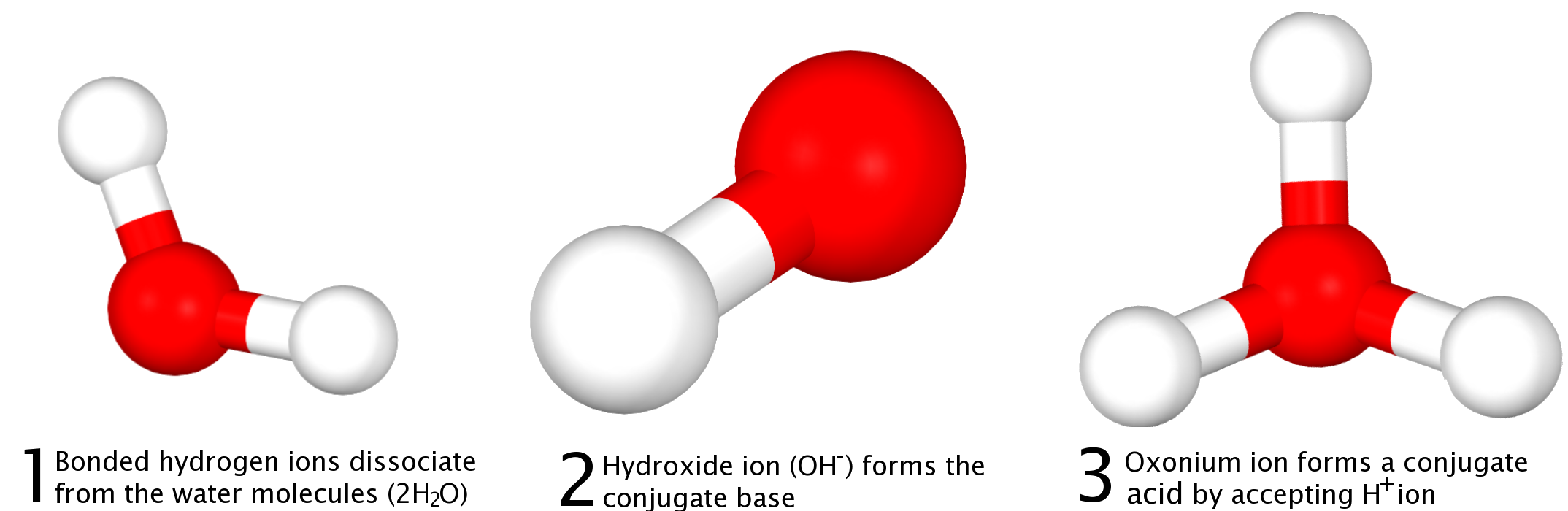
Hydronium is, therefore, the conjugate acid of water, and hydroxide the conjugate base, and both species are in equilibrium with each other. The concentration of water in water does not appear as part of the equilibrium expression, and so what we are left with are the concentrations of the two product molecules { OH }^{ - } and { H }_{ 3 }{ O }^{ 2 }. Because the dissociation constant (K_{ w }) of water is always equal to { 1.0 \times 10 }^{ -14 }, the addition of the pH and pOH of a solution must always equal the negative log of that value, which is 14. That is how we explain the relationship between pH and pOH in solution.
Example 1
What is the concentration of hydronium ion in a 0.500 \text{ L} aqueous solution of 1 \text{ M} sodium hydroxide (NaOH)?
Sodium hydroxide is one of the strong bases and therefore dissociated fully in aqueous solution.
NaOH\rightarrow { Na }^{ + }+{ OH }^{ - }
To find the concentration of hydronium ion, we will need to take advantage of the relationship between pH and pOH of a solution. We begin by calculating the molar amount of sodium hydroxide in the aqueous solution using the unit cancellation method:
\dfrac{1 \text{ mol } OH^-}{1 \text{ L}} \times 0.500 \text{ L} = 0.500 \text{ mol } OH^-
We will then calculate the pOH of the solution.
pOH=-log\left[ { OH }^{ - } \right] = 0.3010
Note that the final number of significant figures has changed. This is because when we take the log of a number, the number of significant figures represents the number of decimal places that must be shown in the logarithm. The reverse is true when going the other direction: the number of decimal places in the log equals the number of significant figures in the number.
We then rearrange the relationship between pH and pOH so solve for the pH of the solution.
pH+pOH=14
pH=14-pOH=14-(0.301)=13.699
Finally, we rearrange the equation for pH to solve for the hydronium ion concentration.
pH=-log\left[ { H }_{ 3 }{ O }^{ + } \right]
\left[ { H }_{ 3 }{ O }^{ + } \right] ={ 10 }^{ -pH }={ 10 }^{ -(13.699) }={ 2.00 \times 10 }^{ -14 } \text{ mol }{ H }_{ 3 }{ O }^{ + }
Qualitatively, this answer makes sense because we expect to have an extremely low concentration of hydronium ions in a basic solution of sodium hydroxide.
One feature of conjugate acids and bases is that they are always weaker than their original counterparts. What does this mean? An acid has a certain ability to donate its proton based on the stability of the fundamental acidic species A, and a base has a certain ability to accept protons based on its ability to stabilize the incoming positive charge. Compounds with pi-systems, such as carboxylic acids and aromatic systems, are generally stronger acids and bases due to their ability to delocalize the electric charge on the molecule.
A Brønsted acid forms an equilibrium mixture when dissolved in water. The water molecule acts as a base, accepting the donated proton from the acid, and becomes the conjugate acid hydronium ion. The acid turns into its deprotonated conjugate base.
HA+{ H }_{ 2 }O\leftrightarrow { H }_{ 3 }{ O }^{ + }+{ A }^{ - }
In this way, Brønsted-Lowry acids are consistent with the Arrhenius definition of an acid because they increase the concentration of { H }_{ 3 }{ O }^{ + } in an aqueous solution. The equilibrium expression for this reaction is called the acid dissociation constant and is designated \left( { K }_{ a } \right). The larger the value of { K }_{ a }, the stronger the acid is. Most weak acids have a dissociation constant in the range of 10^{-2} to 10^{-14}.
{ K }_{ a }=\dfrac { { [{ H }_{ 3 }O^{ + }] }{ [{ A }^{ - }] } }{ { [HA] } }
The acid dissociation constant is a measure of how fully an acid dissociated upon solvation in water. It is a useful measure for the “strength” of an acid, i.e., its ability to stabilize its conjugate base. The acid dissociation constant is often reported as in the negative logarithmic form \left( { pK }_{ a } \right), similar to how pH is reported. The smaller the value of \left( { pK }_{ a } \right), the stronger the acid is. Most weak acids have a \left( { pK }_{ a } \right) between 2 and 14.
{ pK }_{ a } =-log\left( { K }_{ a } \right)
A Brønsted base forms the same equilibrium mixture when dissolved in water, except that here water acts as an acid, donating a proton to becomes the conjugate base hydroxide. This is consistent with the Arrhenius definition of a base, i.e., increasing the concentration of hydroxide ions in aqueous solution. The chemical reaction is expressed as:
B+{ H }_{ 2 }O\leftrightarrow { OH }^{ - }+{ BH }^{ + }
The equilibrium expression for this reaction is called the Base Dissociation Constant and is designated { K }_{ b }. It is a measure of how strongly a base grabs up protons in solution and a good estimate of the strength of a base. The larger the value of { K }_{ b } is, the stronger the base is. Base dissociation constants are also reported as the negative log of { K }_{ b }, and this value is called the { pK }_{ b }. The smaller the value of { pK }_{ b } is, the stronger the base is.
{ K }_{ b }=\dfrac { [{ OH }^{ - }][{ BH }^{ + }] }{ [B] }
Example 2
A given monoprotic acid is dissolved in one liter of water. The acid has a dissociation constant equal to 2 \times 10^{-5}. Calculate the pH of the solution at equilibrium if 0.100 \text{ moles} of the acid are dissolved.
Solving this problem requires us to use ICE tables. For those of you who don’t remember, ICE stands for Initial [Condition], Change, and End[ing Condition]. ICE tables are a common way to solve for equilibrium problems. We write out the balanced chemical equation at the top of the table, and then write the initial concentrations of all reagents, the change in their concentration, and the final concentration. The change is usually represented by the variable x. For the dissociation of an acid in water:
| Equation | HA + | H_2O \rightleftharpoons | H_3O^+ + | A^{-} |
| Initial | 0.100 \text{ mol} | 1 \times 10^{-7} | 0 | |
| Change | -x | +x | +x | |
| End | 0.100 - x | 1 \times 10^{-7} + x | x |
Please note that the equilibrium constant of pure water with hydroxide and hydronium is equal to 1 \times 10^{-14}, so the starting concentration of hydronium (and hydroxide) ions in a solution of pure water is always equal to 1 \times 10^{-7}.
At this point, we substitute the end values into the equilibrium expression for acid dissociation:
{ K }_{ a }=\dfrac { { (1cdot 10^{ -7 }-x) }{ (x) } }{ { (0.100-x) } }
There is a simplifying assumption that we can make if we satisfy certain criteria. In order to avoid calculations involving the quadratic equation, which are both time consuming and tedious, we can make as simple calculation to determine if the value of x in the denominator can be removed. For the simplifying assumption to be true, the initial concentration of the acid divided by the dissociation constant of the acid must be greater than 500. In this case:
\dfrac{0.100}{{ 2 \times 10 }^{ -5 }}=2{,}500
2{,}500 > > 500
We can, therefore, make the simplifying assumption that x in the denominator is negligible. The expression can be further simplified by assuming that the value of x is much greater than the starting concentration of hydronium ion. The final concentration of hydronium in solution can then be simplified simply to x. The equilibrium expression then becomes:
{ K }_{ a }=\dfrac { { ({ x }^{ 2 }) } }{ { (0.100) } }
Substituting in the value for { K }_{ a } allows us to solve for x.
{ K }_{ a }={ 2 \times 10 }^{ -5 }=\dfrac{{ x }^{ 2 }}{0.100}
x={ \left( { 2 \times 10 }^{ -6 } \right) }^{ \dfrac { 1 }{ 2 } }={ 1.41 \times 10 }^{ -3 } \text{ mol}
At this point, we go back and check that our assumption that the value of x is much greater than the starting concentration of hydronium ion by dividing our value by the starting concentration. If the number is greater than 500, then our assumption was good; if not, the assumption is incorrect, and we must go back and consider the hydronium ions initially present in the solution. In this case:
\dfrac{1.4{ 1 \times 10 }^{ -3 }}{{ 1 \times 10 }^{ -7 }} \approx 14{,}000
14{,}000 > > 500
And so our assumption stands. Now to solve the final piece of the puzzle, we substitute the value of x for the concentration of hydronium ions in the pH equation, and arrive at the pH of the acidic solution:
pH=-log({ 1.41 \times 10 }^{ -3 })=2.851
The final equation we will learn relating to acids and bases is the Henderson-Hasselbalch equation, which directly relates the pH of a solution to the { pK }_{ a } of an acid. This equation is useful for calculating the fraction of protonated and deprotonated species of a given acid in a solution of a given pH.
pH=p{ K }_{ a }+log { \dfrac { [{ H }^{ - }] }{ [HA] } }
It makes sense as the concentration of hydronium ions rise in a solution, the acid is less and less likely to become deprotonated by the solvent, and therefore a greater fraction of the acid will exist in the protonated form. The same is true for the reverse. This calculation can also be performed using the base dissociation constant together with the pOH of a solution.
Finally, let us note that the product of the base and acid dissociation constants of a given compound and its conjugate pair is always equal to { K }_{ w } due to the equilibrium that exists between hydronium and hydroxide in aqueous solution.
{ K }_{ w }={ K }_{ a } \times { K }_{ b }={ 1 \times 10 }^{ -14 }
And because of this relationship, the sum of the { pK }_{ a } and { pK }_{ b } of an acid or base and its conjugate pair is always equal to 14.
Looking for AP® Chemistry practice?
Check out our other articles on AP® Chemistry.
You can also find thousands of practice questions on Albert.io. Albert.io lets you customize your learning experience to target practice where you need the most help. We’ll give you challenging practice questions to help you achieve mastery of AP® Chemistry.
Start practicing here.
Are you a teacher or administrator interested in boosting AP® Chemistry student outcomes?
Learn more about our school licenses here.








