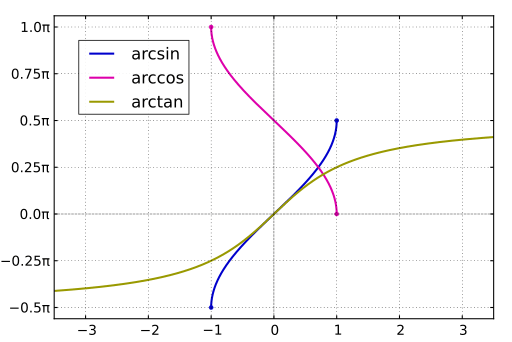
Inverse trig functions might sound intimidating, but they’re just another step in understanding the world of angles and lengths. Think of them as the “undo” for regular trigonometric functions. Mastering these functions is crucial for progressing in precalculus and understanding section 3.9 Inverse Trigonometric Functions in AP® Precalculus.
What We Review
Understanding Inverse Trigonometric Functions
Inverse trig functions help find angles when the trigonometric ratios are given. They switch the roles of inputs and outputs in regular trig functions. The key functions include:
- Arcsine (\sin^{-1} x or \arcsin x )
- Arccosine (\cos^{-1} x or \arccos x )
- Arctangent (\tan^{-1} x or \arctan x )
However, there’s a catch! These functions require restricted domains. This means you can only use certain input values to get a unique output (angle) as a result.
The Arcsine Function: Understanding \arcsin x
Definition and Notation:
- \sin^{-1} x or \arcsin x
- Outputs angles from the range [- \frac{\pi}{2}, \frac{\pi}{2}]
Example 1: Calculating \arcsin \left( \frac{1}{2} \right)
Determine which angle yields a sine of \frac{1}{2}.
- Step 1: Recall the sine value \frac{1}{2} is associated with the well-known angle \frac{\pi}{6}.
- Step 2: Verify the range. \frac{\pi}{6} is within [- \frac{\pi}{2}, \frac{\pi}{2}].
- Solution: \text{arcsin} \left( \frac{1}{2} \right) = \frac{\pi}{6}
Arcsin Graph: It goes from (-1, -\frac{\pi}{2}) to (1, \frac{\pi}{2}) in a well-defined arc.
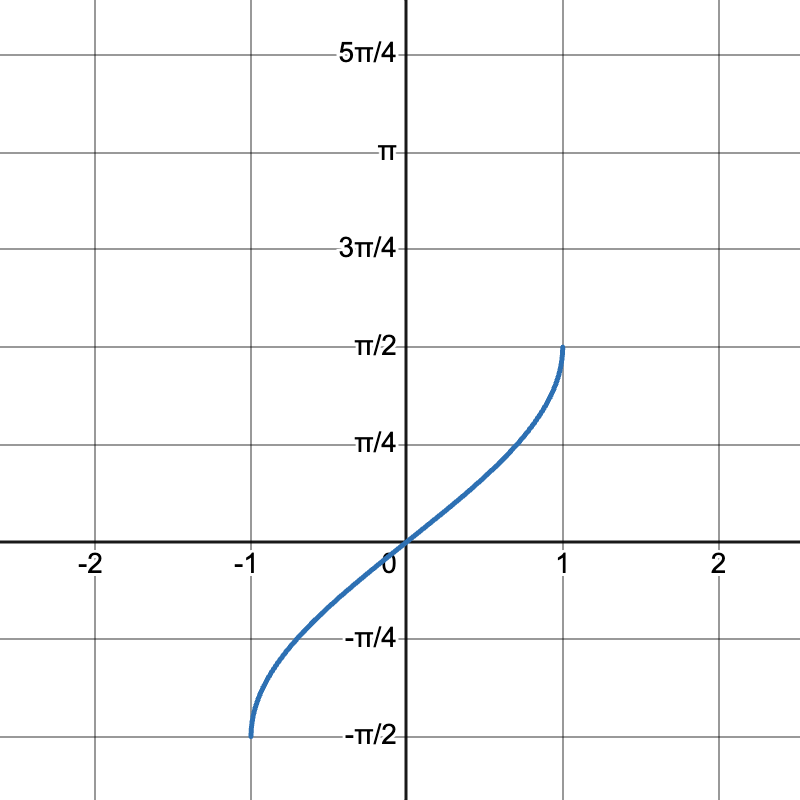
The Arccosine Function: Understanding \arccos x
Definition and Notation:
- \cos^{-1} x or \arccos x
- Outputs angles from the range [0, \pi]
Example 2: Calculating \arccos(1)
Find the angle with a cosine value of 1.
- Step 1: The angle 0 provides a cosine of 1.
- Step 2: Verify the range. 0 is within [0, \pi].
- Solution: \arccos(1) = 0
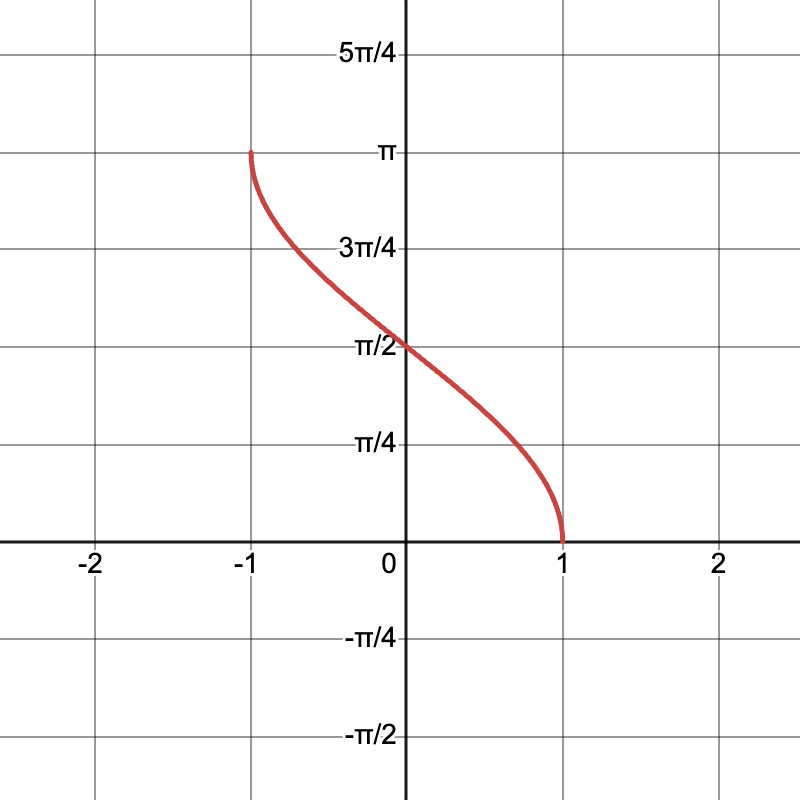
The arccos graph gently drops from (-1, \pi) to (1, 0).
The Arctangent Function: Understanding \arctan x
Definition and Notation:
- \tan^{-1} x or \arctan x
- Outputs angles from the range (- \frac{\pi}{2}, \frac{\pi}{2})
Example 3: Finding \arctan(-1)
Identify the angle with a tangent value of -1.
- Step 1: Recognize that the tangent of -\frac{\pi}{4} is -1.
- Step 2: Verify the range. -\frac{\pi}{4} fits in (- \frac{\pi}{2}, \frac{\pi}{2}).
- Solution: \arctan(-1) = -\frac{\pi}{4}
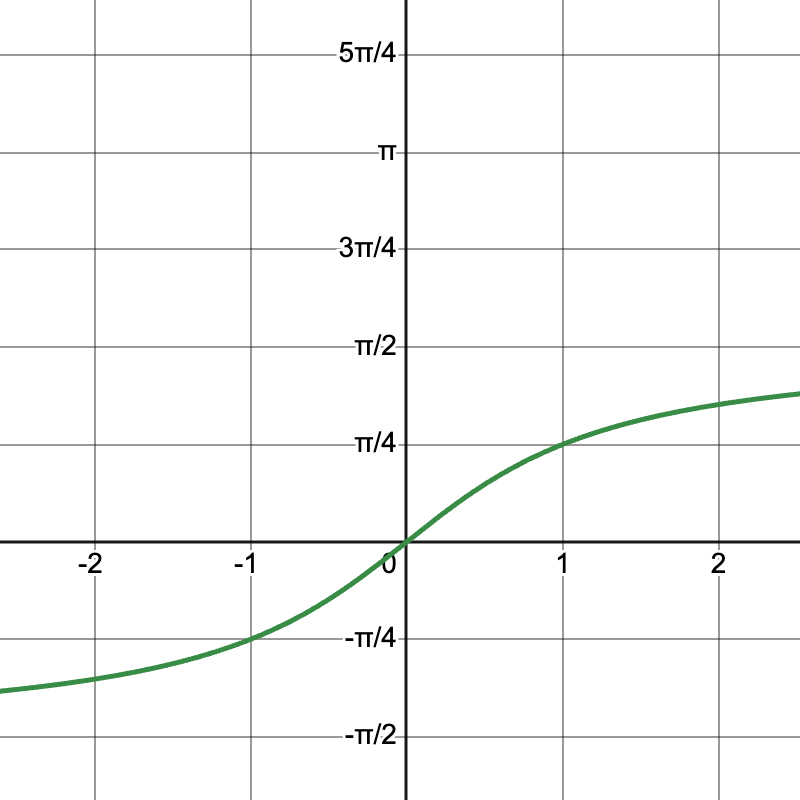
The graph of arctan: Visualize it swooping from the bottom at (-\infty, -\frac{\pi}{2}) to the top at (\infty, \frac{\pi}{2}).
Characteristics and Properties of Inverse Trig Functions
Understanding these relationships aids problem-solving:
- Arcsine links with sine over [- \frac{\pi}{2}, \frac{\pi}{2}].
- Arccosine partners with cosine over [0, \pi].
- Arctangent aligns with tangent over (- \frac{\pi}{2}, \frac{\pi}{2}).
Key properties include:
- Inputs: Know the acceptable values for functions (domains).
- Outputs: Derived angles (ranges) for each function.
Quick Reference Chart
| Function | Notation | Domain | Range |
| Arcsine | \sin^{-1} x | [-1, 1] | [- \frac{\pi}{2}, \frac{\pi}{2}] |
| Arccosine | \cos^{-1} x | [-1, 1] | [0, \pi] |
| Arctangent | \tan^{-1} x | (-\infty, \infty) | (- \frac{\pi}{2}, \frac{\pi}{2}) |
Conclusion
Inverse trigonometric functions might seem challenging, but with practice, they become easier and provide a broader understanding of relationships in math. Dive into more practice to master arcsin, arccos, and arctan for a solid grip on precalculus. Happy learning!
Sharpen Your Skills for AP® Precalculus
Are you preparing for the AP® Precalculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!
Need help preparing for your AP® Precalculus exam?
Albert has hundreds of AP® Precalculus practice questions, free response, and an AP® Precalculus practice test to try out.