Matrix multiplication is a fundamental concept in mathematics that extends beyond the mere manipulation of numbers. Imagine it as a way to combine information from different sources for a more comprehensive view. This article aims to break down basic matrix multiplication rules with step-by-step examples, ensuring you are well-prepared for the AP® Precalculus exam.
What We Review
Understanding Matrices
Definition of a Matrix
A matrix is a rectangular array of numbers, symbols, or expressions arranged in rows and columns. Imagine a matrix as a spreadsheet, where each cell holds a number. The components of a matrix are:
- Rows: Think of these as horizontal lines running across the matrix.
- Columns: These are vertical lines running from top to bottom.
Dimensions of a Matrix
The dimensions of a matrix tell you its size. They are indicated by n \times m , where n is the number of rows and m is the number of columns. For example, a 2 \times 3 matrix has 2 rows and 3 columns.
Requirements for Matrix Multiplication
Conditions for Multiplying Matrices
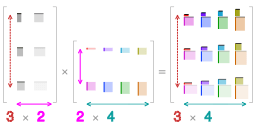
Matrix multiplication isn’t always possible. Before multiplying two matrices, make sure the number of columns in the first matrix equals the number of rows in the second matrix. If matrix A is 3 \times 2 , matrix B must be 2 \times n for multiplication to proceed. Otherwise, the operation is undefined.
Matrix Multiplication: The Process
What is the Product of Two Matrices?
When two matrices are multiplied, the result is a new matrix. The dimensions of this resulting matrix are determined by the rows of the first matrix and the columns of the second. For example, if matrix A is 2 \times 3 and matrix B is 3 \times 4 , the result will be a 2 \times 4 matrix.
Step-by-Step Process
To find each element in the resulting matrix:
- Take a row from the first matrix.
- Take a column from the second matrix.
- Calculate the dot product:
Multiply corresponding elements and sum them to get one element of the resultant matrix.
Example 1: Multiplication of 2×2 Matrix
Consider matrices A and B where:
A = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}, \quad B = \begin{bmatrix} 5 & 6 \\ 7 & 8 \end{bmatrix}Let’s multiply A and B:
- To find the element in the first row and first column of the product, calculate: (1 \cdot 5) + (2 \cdot 7) = 5 + 14 = 19
- For the first row, second column: (1 \cdot 6) + (2 \cdot 8) = 6 + 16 = 22
- For the second row, first column: (3 \cdot 5) + (4 \cdot 7) = 15 + 28 = 43
- For the second row, second column: (3 \cdot 6) + (4 \cdot 8) = 18 + 32 = 50
Thus, the product AB = \begin{bmatrix} 19 & 22 \\ 43 & 50 \end{bmatrix}
Example 2: Multiplication of Matrix 3×3
Now, consider:
C = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix}, \quad D = \begin{bmatrix} 9 & 8 & 7 \\ 6 & 5 & 4 \\ 3 & 2 & 1 \end{bmatrix}Calculate (i, j) elements in similar steps. Example: For first row, first column:
(1 \cdot 9) + (2 \cdot 6) + (3 \cdot 3) = 9 + 12 + 9 = 30Continue for the remaining elements to complete:
CD = \begin{bmatrix} 30 & 24 & 18 \\ 84 & 69 & 54 \\ 138 & 114 & 90 \end{bmatrix}Common Mistakes in Matrix Multiplication
Avoid these traps:
- Mismatched dimensions: Verify row-column compatibility.
- Incorrect dot product: Ensure precise element-wise multiplication and addition.
Practical Applications of Matrix Multiplication
Matrix multiplication extends far beyond math classes. In computer science, matrices are crucial for graphics transformations. In economics, they help run complex data simulations. Additionally, engineers employ matrices for systems modeling in various fields.
Quick Reference Chart
| Term | Definition |
| Matrix | Rectangular array of numbers arranged in rows and columns |
| Dimensions | Size of a matrix denoted by n \times m |
| Dot Product | Sum of the products of corresponding elements from a row and column during multiplication |
| Product Matrix | Matrix resulting from the multiplication of two matrices |
Conclusion
Mastering matrix multiplication is vital for tackling advanced math and real-world problems. Practice will cement these concepts, allowing them to be applied effectively in various scenarios.
Understanding matrix multiplication equips you with a powerful tool for both academic success and practical applications. Continue practicing and exploring its vast potential.
Sharpen Your Skills for AP® Precalculus
Are you preparing for the AP® Precalculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!
Need help preparing for your AP® Precalculus exam?
Albert has hundreds of AP® Precalculus practice questions, free response, and an AP® Precalculus practice test to try out.









