Understanding exponents is essential for tackling section 2.4 Exponential Function Manipulation in AP® Precalculus. Exponents make it easier to manage large numbers and express repeated multiplication. This article focuses on negative exponents and properties associated with exponents. Let’s simplify these concepts step by step.
What We Review
Understanding Negative Exponents
Definition of Negative Exponents: A negative exponent property tells us to take the reciprocal of the base and apply the positive exponent. The property is given by:
b^{-n} = \frac{1}{b^n}
Why We Use Negative Exponents: Negative exponents help rewrite exponential expressions to express a decrease or inverse.
Example: Rewrite ( 2^{-3} ).
- Step 1:Identify the base and the exponent. Here, the base is 2, and the exponent is -3.
- Step 2: Apply the negative exponent property.
- Step 3: Solution: 2^{-3} = \frac{1}{2^3} = \frac{1}{8}
Practice Problem: Rewrite ( 5^{-2} ). Solution: \frac{1}{25}
The Product Property of Exponents
Introduction to the Product Property: When multiplying powers with the same base, add the exponents:
b^m \cdot b^n = b^{(m+n)}
Using This Property: It simplifies expressions by reducing multiple terms to a single term with one exponent.
Example: Simplify ( 3^2 \cdot 3^4 ).
- Step 1:Identify the bases and add the exponents. The base is 3, and the exponents are 2 and 4.
- Step 2: Application: 3^{(2+4)} = 3^6 = 729
Practice Problem: Simplify ( 4^1 \cdot 4^3 ). Solution: ( 4^4 )
The Power Property of Exponents
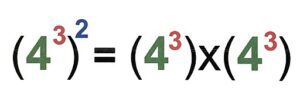
Explanation of the Power Property: When raising a power to another power, multiply the exponents:
(b^m)^n = b^{(m \cdot n)}
When to Use This Property: This is useful for simplifying expressions with nested exponents.
Example: Simplify ( (5^2)^3 ).
- Step 1:Multiply the exponents: 2 and 3.
- Step 2: Result: 5^{(2 \cdot 3)} = 5^6 = 15625
Practice Problem: Simplify ( (2^3)^4 ). Solution: ( (2^{12} )
Transitioning to Units and Roots
Understanding Exponential Unit Fractions: These expressions represent roots. For example, ( b^{(\frac{1}{k})} ) means the k-th root of b.
Example: Simplify ( 16^{(\frac{1}{4})} ).
- Step 1: Recognize that this is the fourth root of 16.
- Step 2: Solution: 16^{(\frac{1}{4})} = 2 (because ( 2^4 = 16 ))
Practice Problem: Simplify ( 27^{(\frac{1}{3})} ). Solution: ( 3)
Application of Properties
Combining the properties discussed above enables the simplification of complex exponential expressions.
Example: Simplify ( \frac{4^{-2} \cdot 2^5}{8^{-1}} ).
- Step 1: Apply the negative exponent property to rewrite each negative exponent.
- Step 2: Calculate each component: 4^{-2} = \frac{1}{16}, \quad 2^5 = 32, \quad 8^{-1} = \frac{1}{8}
- Step 3: Combine and simplify: \frac{1/16 \cdot 32}{1/8} = 16
Practice Problem: Simplify ( \frac{10^{-1} \cdot 5^3}{25^{-2}} ). Solution: ( \frac{5^7}{10} )
Quick Reference Chart
| Vocabulary Term | Definition |
| Negative Exponent | ( b^{-n} = \frac{1}{b^n} ) |
| Product Property | ( b^m \cdot b^n = b^{(m+n)} ) |
| Power Property | ( (b^m)^n = b^{(m \cdot n)} ) |
| Exponential Unit Fraction | ( b^{\frac{1}{k}} ) is the ( k^{th} ) root of ( b ) |
Conclusion
Mastering negative exponents and their properties makes algebra more manageable and enjoyable. Practicing these concepts builds confidence for assessments and future math challenges. Explore more resources and practice problems to strengthen understanding.
Sharpen Your Skills for AP® Precalculus
Are you preparing for the AP® Precalculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!
Need help preparing for your AP® Precalculus exam?
Albert has hundreds of AP® Precalculus practice questions, free response, and an AP® Precalculus practice test to try out.









