Welcome to the fascinating world of electrical principles, where understanding Ohm’s Law is not just a skill but a necessity. Often considered the backbone of electrical engineering and physics, Ohm’s Law is a fundamental concept that illuminates the relationship between voltage, current, and resistance in an electrical circuit. In this comprehensive guide, we will cover the core of Ohm’s Law, explore its fundamental formula, and work through a series of Ohm’s Law practice problems. Mastering Ohm’s Law is a step towards unraveling the complexities of electronics.

What Does Ohm’s Law State?

Ohm’s Law is a fundamental principle in electronics and physics, providing a simple yet powerful way to understand the relationship between voltage, current, and resistance in electrical circuits. At its core, Ohm’s Law states that the current through a conductor between two points is directly proportional to the voltage across these points and inversely proportional to the resistance between them. This relationship is elegantly captured in the formula $V = IR$, where $V$ stands for voltage, $I$ for current, and $R$ for resistance.

Understanding Voltage, Current, and Resistance

In order to fully appreciate Ohm’s law, let’s review the three components.

• Voltage (V): Often described as the electrical force or pressure that drives the flow of electrons through a conductor. It’s the potential difference between two points in a circuit.
• Current (I): This is the flow of electrical charge, measured in amperes (A). It represents how many electrons are flowing through the circuit.
• Resistance (R): Resistance is the opposition to the current flow in a circuit. It’s measured in ohms (Ω) and depends on the material, size, and temperature of the conductor.

By manipulating the Ohm’s Law formula, you can solve for any one of these three variables if the other two are known. This makes it an invaluable tool for understanding and designing electrical circuits.

Practical Applications

Ohm’s Law isn’t just a theoretical concept; it has numerous practical applications in everyday life and various industries. Here are a few examples:

• Electronics Design: Engineers use Ohm’s Law to design circuits, select appropriate components, and ensure electrical devices function safely and efficiently.
• Troubleshooting Electrical Problems: Technicians often use Ohm’s Law to diagnose issues in electrical systems, such as finding short circuits or identifying components that are not functioning correctly.
• Educational Purposes: Ohm’s Law is a fundamental concept taught in physics and electronics courses, helping students understand the basics of electrical circuits.
• Power Management: In larger-scale applications like power distribution, Ohm’s Law helps calculate the load that can be safely put on electrical systems without causing damage or inefficiency.

Understanding Ohm’s Law opens up possibilities for creating, managing, and troubleshooting electrical systems, from the smallest electronic devices to large-scale power grids.

What is the Formula for Ohm’s Law?

Ohm’s Law is elegant in its formulation, providing a precise mathematical relationship between voltage, current, and resistance in an electrical circuit.

Ohm’s Law Formula $V = IR$

In the formula for Ohm’s Law, $V$ represents voltage measured in volts (V), $I$ is the current measured in amperes (A), and $R$ is the resistance measured in ohms (Ω). This formula is the cornerstone for analyzing and understanding electrical circuits, requiring two variables to solve.

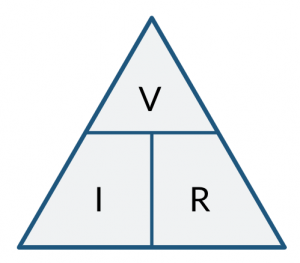
Ohm’s Law Triangle

The Ohm’s Law triangle is a helpful tool for remembering how to calculate voltage, current, and resistance. It visually represents the formula $V=IR$ in a graphic format, with $V$ at the top, $I$ on the left, and $R$ on the right. By covering the variable you want to calculate, the other two variables show how they relate. For example, covering $V$ shows $I\times R$, covering $I$ shows $/frac{V}{R}$, and covering $R$ shows $\frac{V}{I}$. This tool is handy for beginners and a reference for quick calculations.

Strategies for Solving Ohm’s Law Practice Problems

When solving problems using Ohm’s Law, it’s important to follow a systematic approach:

• Identify Known Quantities: Start by determining which of the three variables (voltage, current, resistance) are known.
• Determine the Unknown: Figure out which variable you need to calculate.
• Use the Ohm’s Law Circle: Utilize the Ohm’s Law circle to understand the relationship between the variables and to choose the correct formula.
• Solve Step-by-Step: Apply the formula and solve for the unknown variable step-by-step, ensuring accuracy in your calculations.
• Check Units: Always check that your units are consistent (volts for voltage, amperes for current, ohms for resistance) and convert if necessary.

By applying these strategies, you can effectively use Ohm’s Law to solve a wide range of electrical problems, enhancing your understanding and skills in electrical theory and practice.

Examples of Ohm’s Law

Calculating Current: If a light bulb has a resistance of $240\text{ ohms}$ and is connected to a $120\text{-volt}$ power source, the current flowing through it can be calculated as:

$V = IR$ is rearranged to become $I = \frac{V}{R}$

$I = \frac{V}{R} = \frac{120\text{ V}}{240\ \Omega} = 0.5\text{ A}$

Determining Voltage: For a toaster that draws a current of $5\text{ amperes}$ and has a resistance of $10\text{ ohms}$, the voltage across it is:

$V = IR = 5\text{ A} \times 10 \ \Omega = 50\text{ V}$

Finding Resistance: If a hairdryer operates at $220\text{ volts}$ and draws a current of $11\text{ amperes}$, its resistance is:

$V = IR$ is rearranged to become $R = \frac{V}{I}$

$R = \frac{V}{I} = \frac{220\text{ V}}{11 \text{ A}} = 20 \ \Omega$

These examples demonstrate how Ohm’s Law is applied in practical situations, providing a clear understanding of how electrical components function in various devices.

Ohm’s Law Practice Problems

Here are eight practice problems involving Ohm’s Law, arranged in order of increasing complexity. These problems will help you apply the concepts of voltage, current, and resistance in various scenarios. Work through these on your own, then scroll down for solutions.

1. Basic Current Calculation

A circuit with a $9\text{-volt}$ battery and a resistor of $3\text{ ohms}$. What is the current flowing through the circuit?

2. Resistance Determination

Find the resistance of a bulb that draws $0.5\text{ amperes}$ from a $120\text{-volt}$ supply.

3. Voltage Calculation

What is the voltage across a resistor of $15\text{ ohms}$ through which a current of $2\text{ amperes}$ is flowing?

4. Multiple Resistors (Series) 

In a series circuit with a $12\text{-volt}$ battery, if there are two resistors of $4\text{ ohms}$ and $6\text{ ohms}$, what is the current flowing through the circuit?

5. Multiple Resistors (Parallel)

Calculate the total resistance in a parallel circuit with two resistors of $5\text{ ohms}$ and $10\text{ ohms}$. If a voltage of $12\text{-volts}$ is applied across the circuit, what is the total current flowing through the circuit?

6. Combined Ohm’s Law and Power

A device using $18\text{ watts}$ of power is connected to a $9\text{-volt}$ battery. Calculate the current drawn by the device and determine the resistance of the device.

7. Variable Resistance

If the current in a circuit is $0.25\text{ amperes}$ and the voltage is $10\text{ volts}$, what must be the resistance?

8. Complex Circuit Analysis

In a circuit, a $6\text{-ohm}$ resistor and a $12\text{-ohm}$ resistor are connected in series to a $9\text{-volt}$ battery. Calculate the current through each resistor.

Solutions to Ohm’s Law Practice Problems

Are you ready to see how you did? Review below to see the solutions for the Ohm’s Law practice problems.

1. Basic Current Calculation

A circuit with a $9\text{-volt}$ battery and a resistor of $3\text{ ohms}$. What is the current flowing through the circuit?

We have a simple circuit with a $9\text{ V}$ battery and a $3\ \Omega$ resistor. In order to solve this, use Ohm’s Law, $V=IR$ to find the current:

$V = IR$ is rearranged to become $I = \frac{V}{R}$

$I = \frac{V}{R} = \frac{9\text{ V}}{3\ \Omega} = 3\text{ A}$

Therefore, the current flowing through this circuit is $3\text{ amperes}$, typical for small electronic devices.

2. Resistance Determination

Find the resistance of a bulb that draws $0.5\text{ amperes}$ from a $120\text{-volt}$ supply.

A bulb is connected to a $120\text{ V}$ supply and draws $0.5\text{ A}$.To find the resistance, rearrange Ohm’s Law to $R = V/I$:

$V = IR$ is rearranged to become $R = \frac{V}{I}$

$R = \frac{V}{I} = \frac{120\text{ V}}{0.5 \text{ A}} = 240 \ \Omega$

The bulb has a resistance of $240\ \Omega$, indicating it’s suitable for moderate power applications.

3. Voltage Calculation

What is the voltage across a resistor of $15\text{ ohms}$ through which a current of $2\text{ amperes}$ is flowing?

A resistor of $15\ \Omega$ carries a current of $2\text{ A}$. Apply $V=IR$ to find the voltage across the resistor:

$V = IR = 2\text{ A} \times 15 \ \Omega = 30\text{ V}$

The voltage across this resistor is $30\text{ V}$, typical for small household circuits.

4. Multiple Resistors (Series) 

In a series circuit with a $12\text{-volt}$ battery, if there are two resistors of $4\text{ ohms}$ and $6\text{ ohms}$, what is the current flowing through the circuit?

We have a series circuit with a $12\text{ V}$ battery and two resistors ($4\ \Omega$ and $6\ \Omega$). First, sum the resistances in series. Then, apply Ohm’s Law.

Summing the resistance:

$R_{total} = R_1 + R_2 = 4\ \Omega + 6\ \Omega = 10\ \Omega$

Now, apply Ohm’s Law with the total resistance, rearranged for the current:

$V = IR$ is rearranged to become $I = \frac{V}{R}$

$I = \frac{V}{R} = \frac{12\text{ V}}{10\ \Omega} = 1.2\text{ A}$

The current of $1.2\text{ A}$ flows uniformly through each component in this series circuit.

5. Multiple Resistors (Parallel)

Calculate the total resistance in a parallel circuit with two resistors of $5\text{ ohms}$ and $10\text{ ohms}$. If a voltage of $12\text{-volts}$ is applied across the circuit, what is the total current flowing through the circuit?

In this scenario, there is a parallel circuit with two resistors of $5\ \Omega$ and $10\ \Omega$. First, calculate the total resistance in parallel using the reciprocal formula:

$\dfrac{1}{R_{total}} = \dfrac{1}{R_1} + \dfrac{1}{R_2} = \dfrac{1}{5\ \Omega}+\dfrac{1}{10\ \Omega}$

$R_{total} = \dfrac{1}{\dfrac{1}{5\ \Omega}+\dfrac{1}{10\ \Omega}} = 3.3\ \Omega$

Then, apply Ohm’s Law with the total resistance, rearranged for the current:

$V = IR$ is rearranged to become $I = \frac{V}{R}$

$I = \frac{V}{R} = \frac{12\text{ V}}{3.3\ \Omega} = 3.6\text{ A}$

The total current flowing through the circuit is approximately $3.6\text{ A}$.

6. Combined Ohm’s Law and Power

A device using $18\text{ watts}$ of power is connected to a $9\text{-volt}$ battery. Calculate the current drawn by the device and determine the resistance of the device.

An $18\text{ W}$ device is connected to a $9\text{ V}$ battery. First, find the current using by rearranging the power formula $P=VI$:

$P = IV$ is rearranged to become $I = \frac{P}{V}$

$I = \frac{P}{V} = \frac{18\text{ W}}{9\text{ V}} = 2\text{ A}$

The device draws a current of $2\text{ A}$. Next, use Ohm’s Law rearranged for resistance:

$V = IR$ is rearranged to become $R = \frac{V}{I}$

$R = \frac{V}{I} = \frac{9\text{ V}}{2 \text{ A}} = 4.5 \ \Omega$

The device’s resistance is $4.5\ \Omega$.

7. Variable Resistance

If the current in a circuit is $0.25\text{ amperes}$ and the voltage is $10\text{ volts}$, what must be the resistance?

For a circuit with a current of $0.25\text{ A}$ and a voltage of $10\text{ V}$, apply Ohm’s Law to find the resistance:

$V = IR$ is rearranged to become $R = \frac{V}{I}$

$R = \frac{V}{I} = \frac{10\text{ V}}{0.25 \text{ A}} = 40 \ \Omega$

The circuit has a resistance of $40\ \Omega$, indicating a relatively high resistance for the given current and voltage.

8. Complex Circuit Analysis

In a circuit, a $6\text{-ohm}$ resistor and a $12\text{-ohm}$ resistor are connected in series to a $9\text{-volt}$ battery. Calculate the current through each resistor.

First, calculate the total resistance:

$R_{total} = R_1 + R_2 = 6\ \Omega + 12\ \Omega = 18\ \Omega$

Then, apply Ohm’s Law with the total resistance, rearranged for the current:

$V = IR$ is rearranged to become $I = \frac{V}{R}$

$I = \frac{V}{R} = \frac{9\text{ V}}{18\ \Omega} = 0.5\text{ A}$

For a series circuit, all elements receive the same current. Each resistor in this series circuit experiences a current of $0.5\text{ A}$.

Conclusion

As we reach the end of our exploration into Ohm’s Law, it’s clear that this fundamental principle is more than just a formula; it’s a key to unlocking the mysteries of electrical circuits. Through this guide, we’ve journeyed from the basic understanding of voltage, current, and resistance to applying these concepts in various practical scenarios. The practice problems provided various challenges, from straightforward calculations to more complex circuit analyses, each designed to strengthen your grasp of Ohm’s Law.

Remember, the journey of mastering Ohm’s Law is as much about practice as it is about understanding the theory. Each problem you solve, and each circuit you analyze adds to your skill set, making you more adept at navigating the world of electronics.