What We Review
Introduction
Coordinate systems are essential in mathematics. They give us ways to pinpoint locations on a graph. Two common systems are polar coordinates and rectangular coordinates. Understanding these systems is crucial for mastering concepts in 3.13 trigonometry and polar coordinates.
Understanding Rectangular Coordinates
Rectangular coordinates, also known as Cartesian coordinates, use an ordered pair ((x, y)). Here, (x) is the horizontal position and (y) is the vertical position on the graph.
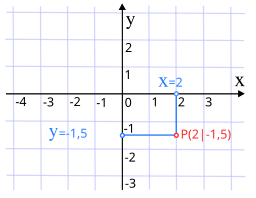
- Structure: ((x, y)) where both (x) and (y) are real numbers
- Graphing Points: To graph a point, move horizontally by (x) units from the origin and vertically by (y) units.
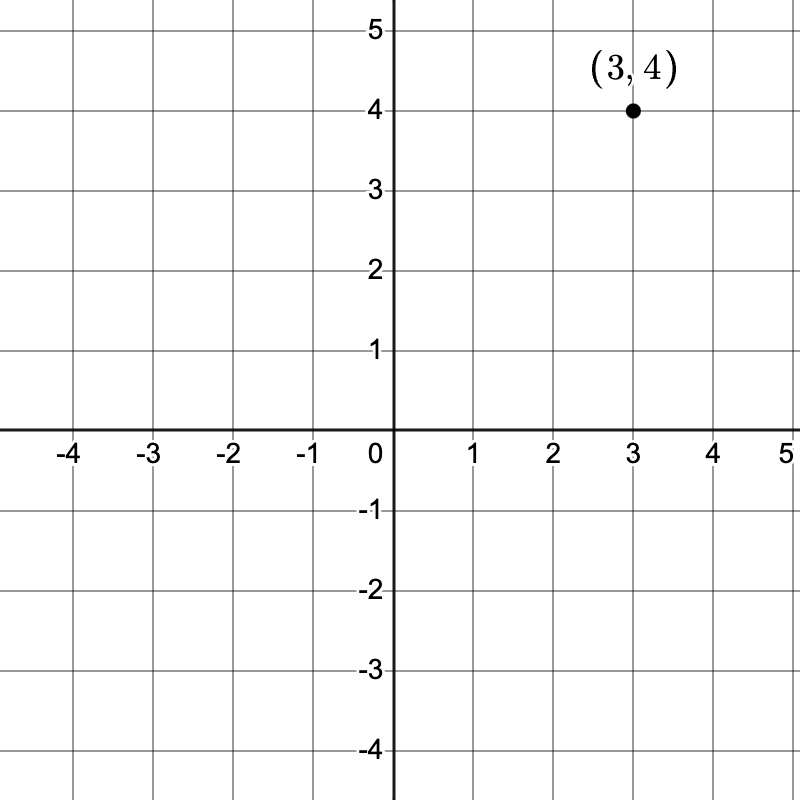
Example: Plotting the Point (3, 4)
- Start at the origin ((0, 0)).
- Move 3 units to the right (because (x = 3)).
- Move 4 units up (because (y = 4)).
- Mark the point.
Exploring Polar Coordinates
Polar coordinates use a different system. An ordered pair ((r, \theta)) shows a point’s position based on distance and angle from the origin.
- Structure: ((r, \theta))
- (r): Distance from the origin, or radius.
- (\theta): Angle from the positive x-axis, often in degrees or radians.
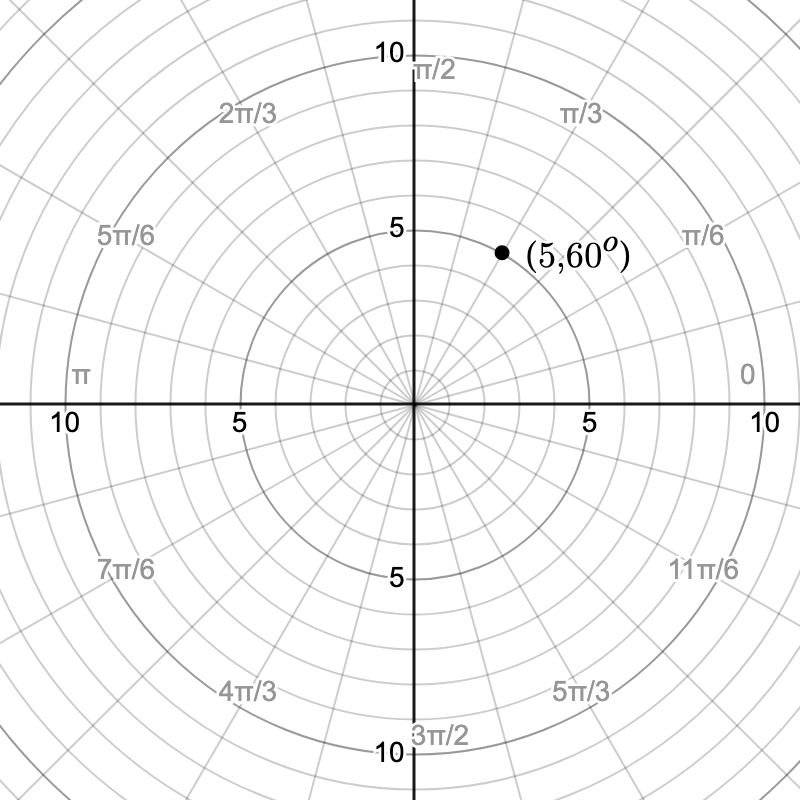
Example: Plotting the Point (5, 60°)
- Identify the radius (r = 5).
- Find the angle (\theta = 60^\circ).
- Draw a line at a 60° angle from the positive x-axis.
- Measure 5 units along this line.
- Mark the point.
Converting Between Coordinate Systems
Sometimes, it’s handy to switch between these coordinate systems. Here’s how:
From Polar to Rectangular Coordinates
Use the formulas:
- x = r \cos \theta
- y = r \sin \theta
Example: Converting (3, 45°) to Rectangular Coordinates
- x = 3 \cos 45^\circ = 3 \times \frac{\sqrt{2}}{2} \approx 2.12
- y = 3 \sin 45^\circ = 3 \times \frac{\sqrt{2}}{2} \approx 2.12
- Result: ((2.12, 2.12))
From Rectangular to Polar Coordinates
Use the formulas:
- r = \sqrt{x^2 + y^2}
- \theta = \arctan \frac{y}{x}
Example: Converting (3, 4) to Polar Coordinates
- r = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = 5
- \theta = \arctan \frac{4}{3} \approx 53.13^\circ
- Result: ((5, 53.13^\circ))
Visualizing Polar and Rectangular Coordinates
Both systems offer benefits. Rectangular coordinates suit linear movements in grids, like in graph plotting. Polar coordinates help in circular movements and scenarios involving angles.
Applications:
- Rectangular suits navigation in grids.
- Polar is beneficial for physics problems involving circular motion.
Complex Numbers and Coordinate Systems
Complex numbers can be viewed in both rectangular and polar forms.
- Rectangular Form: a + bi
- Polar Form: r(\cos \theta + i \sin \theta) = r \text{cis} \theta
Example: Converting (3 + 4i) into Polar Form
- r = \sqrt{3^2 + 4^2} = 5
- \theta = \arctan \frac{4}{3} \approx 53.13^\circ
- Result: 5 \text{ cis } 53.13^\circ
Summary of Key Concepts
Quick Reference Chart:
| Term | Definition |
| Rectangular Coordinates | Ordered pair ((x, y)) |
| Polar Coordinates | Ordered pair ((r, \theta)) |
| Radius (r) | Distance from the origin in polar coordinates |
| Angle (\theta) | Angle measured from the positive x-axis |
| Complex Number | Number in the form (a + bi) |
| (\text{ cis } \theta) | Short for (\cos \theta + i \sin \theta) |
Conclusion
Understanding the difference between polar and rectangular coordinates is crucial in various fields, especially in trigonometry and graphing. Practice converting and visualizing these systems. Doing so will bolster mathematical skills and provide insight into real-world applications.
Sharpen Your Skills for AP® Precalculus
Are you preparing for the AP® Precalculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!
Need help preparing for your AP® Precalculus exam?
Albert has hundreds of AP® Precalculus practice questions, free response, and an AP® Precalculus practice test to try out.









