Whether you’re new to solving multi-step equations or simply studying before that big chapter test, Albert has you covered!
This blog post will guide you through defining multi-step equations, examples of multi-step equations, and how to solve multi-step equations (including problems with fractions and words). Let’s go!
Return to the Table of Contents
What We Review
What is a multi-step equation?
Remember, an equation is a mathematical sentence that uses an equal sign, = , to show that two expressions are equal.
We began our study of solving equations with one-step equations, then we moved on to two-step equations. (Check out those links if you need a quick refresher!)
Now we are moving to multi-step equations. A multi-step equation is an equation that takes two or more steps to solve. These problems can have a mix of addition, subtraction, multiplication, or division. We also might have to combine like terms or use the distributive property to properly solve our equations.
So get your mathematical toolbox out! You never know what you might see in a multi-step equation!

Examples of multi-step equations
Multi-step equations are a wide-ranging category of equations. Some can be very simple, while others become more complex. Never fear! We’re going to show you many examples of multi-step equations and how to solve these important aspects of Algebra 1.
Here are some examples of multi-step equations:
5x + 10 = 3x + 12
8y - 3 - 2y = 5
4(3m - 2) = 16
5x - 10 + 5 = 20 - 5x
Return to the Table of Contents
How to solve multi-step equations
Remember, an equation is solved when we have isolated the variable and found a value that makes the equation true. In order to solve equations, we use inverse operations to help us isolate the variable.
\text{Addition} \leftrightarrow \text{Subtraction}
\text{Multiplication} \leftrightarrow \text{Division}
Order of Operations
Another mathematical concept that will help when solving multi-step equations is the Order of Operations. To use the order of operations, we must first do any operations inside grouping symbols (parentheses, brackets, etc), then exponents, then multiplication or division (whatever comes first, left to right), then finally addition or subtraction (whatever comes first, left to right). You can remember this by the acronym, PEMDAS.
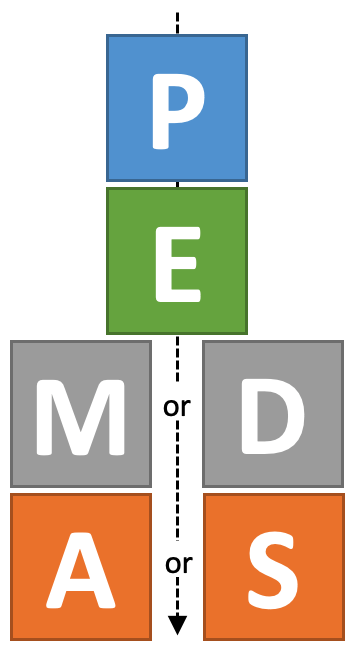
Additionally, we may have to combine like terms on either side of the equation to help solve these equations. Eventually, you will create a one- or two-step equation that you will be able to solve similarly to previous problems!
Here is an example of a multi-step equation with variables on both sides:
Solve for x in the following equation:
| 8x - 10 = 4x + 2 | Original equation |
Since there are variables on both sides, we must eliminate the variable from one side first. I suggest moving the 4x first, as to not create a negative.
| 8x - 4x - 10 = 4x - 4x + 2 | Subtract 4x from each side |
| 4x - 10 = 2 | Simplify |
Now we are back to a basic two-step equation.
| 4x - 10 + 10 = 2 + 10 | Add 10 from each side |
| 4x = 12 | Simplify |
| \dfrac{4x}{4} = \dfrac{12}{4} | Divide each side by 4 |
| x = 3 | Simplify |
To check you answer, you can simplify substitute 3 into the variable to see if the equation is true:
| 8x - 10 = 4x + 2 | Original equation |
| 8(3) - 10 = 4(3) + 2 | Substitute |
| 24 - 10 = 12 + 2 | Simplify |
| 14 = 14 \checkmark | Answer confirmed |
Thus, x = 3 is the correct solution.
Return to the Table of Contents
Below is a short video from Mike DeVor showing more examples of solving multi-step equations:

Now that we have been introduced to Multi-Step Equations, let’s get those brain gears in motion and look at some more challenging examples!
Multi-step equations with fractions
When dealing with an equation with more than one fraction, the easiest way to solve the equation is by finding the Least Common Denominator. The least common denominator is the smallest number that can be a common denominator for a set of fractions.
Once we find the least common denominator, we will multiply each term by this value to eliminate the fraction. Here is an example of a multi-step equation with fractions:
Solve for y in the following equation:
\dfrac{5y}{6} - \dfrac{1}{4} = \dfrac{3y}{4} + \dfrac{1}{2}
The denominators above are 2, 4, 6 , therefore the least common denominator for these numbers is 12 . So we will multiply each term by 12 .
| 12 \cdot \dfrac{5y}{6} - 12 \cdot \dfrac{1}{4} = 12 \cdot \dfrac{3y}{4} + 12 \cdot \dfrac{1}{2} | Multiply each term by 12 |
| \dfrac{60y}{6} - \dfrac{12}{4} = \dfrac{36y}{4} + \dfrac{12}{2} | Result of multiplication |
| 10y - 3 = 9y + 6 | Simplify |
| 10y - 9y - 3 = 9y - 9y + 6 | Subtract 9y from each side |
| y - 3 = 6 | Simplify |
| y - 3 + 3 = 6 + 3 | Add 3 to each side |
| y = 9 | Simplify |
To check your answer, you can substitute 9 into the variable to see if the equation is true:
| \dfrac{5y}{6} - \dfrac{1}{4} = \dfrac{3y}{4} + \dfrac{1}{2} | Original equation |
| 10y - 3 = 9y + 6 | Simplified equation (all terms multiplied by 12 ) |
| 10 \cdot 9 - 3 = 9 \cdot 9 + 6 | Substitute |
| 90 - 3 = 81 + 6 | Simplify |
| 87 = 87 \checkmark | Answer confirmed |
Therefore, y = 9 is the correct solution.
Return to the Table of Contents
Multi-step equations with distributive property
Example 1
Solve for z in the following equation:
| 2(3z - 4) = 10 | Original equation |
| 2(3z) - 2(4) = 10 | Distributive Property |
| 6z - 8 = 10 | Simplify |
| 6z - 8 + 8 = 10 + 8 | Add 8 to each side |
| 6z = 18 | Simplify |
| \dfrac{6z}{6} = \dfrac{18}{6} | Divide each side by 6 |
| z = 3 | Simplify |
To check you answer, you can substitute 3 into the variable to see if the equation is true:
| 2(3z - 4) = 10 | Original equation |
| 2(3 \cdot 3 - 4) = 10 | Substitute |
| 2(9 - 4) = 10 | Simplify |
| 2(5) = 10 | Simplify |
| 10 = 10 \checkmark | Answer confirmed |
Thus, z = 3 is the correct solution.
Example 2
Solve for m in the following equation:
| 3(m + 3) - 4 = 2(m - 2) | Original equation |
| 3(m) + 3(3) - 4 = 2(m) - 2(2) | Distributive Property |
| 3m + 9 - 4 = 2m - 4 | Simplify |
| 3m + 5 = 2m - 4 | Combine like terms |
| 3m - 2m + 5 = 2m - 2m - 4 | Subtract 2m from each side |
| m + 5 = - 4 | Simplify |
| m + 5 - 5 = - 4 - 5 | Subtract 5 from each side |
| m = -9 | Simplify |
To check you answer, you can simplify substitute -9 into the variable to see if the equation is true:
| 3(m + 3) - 4 = 2(m - 2) | Original equation |
| 3(-9 + 3) - 4 = 2(-9 - 2) | Substitute |
| 3(-6) - 4 = 2(-11) | Simplify |
| -18 - 4 = -22 | Combine like terms |
| -22 = -22 \checkmark | Answer confirmed |
Thus, m = -9 is the correct solution.
Return to the Table of Contents
Multi-step equation word problems
Example 1
| Rob owns a coffee shop and is looking at finding a new coffee distributor for his beans. Distributor A sells their beans for \$5 a pound, plus a flat \$10 shipping fee. Distributor B sells their beans for \$2 a pound, plus \$1 per pound for shipping, plus a \$40 processing fee. What amount of pounds, p , would be a breakeven point for the two companies? |
Solution
First, let’s create an equation for the situation:
| 5p + 10 = 2p + 1p + 40 | Original equation |
| 5p + 10 = 3p + 40 | Combine like terms |
| 5p -3p + 10 = 3p - 3p + 40 | Subtract 3p from each side |
| 2p + 10 = 40 | Simplify |
| 2p + 10 - 10 = 40 - 10 | Subtract 10 from each side |
| 2p = 30 | Simplify |
| \dfrac{2p}{2} = \dfrac{30}{2} | Divide each side by 2 |
| p = 15 | Simplify |
To check you answer, you can simplify substitute 15 into the variable to see if the equation is true:
| 5p + 10 = 2p + 1p + 40 | Original equation |
| 5(15) + 10 = 2(15) + 1(15) + 40 | Substitute |
| 75 + 10 = 30 + 15 + 40 | Simplify |
| 85 = 85 \checkmark | Answer confirmed |
Therefore, the breakeven point for Distributor A and Distributor B would be 15 pounds.
Example 2
| Sam goes to a bookstore with a coupon for \$5 off a book. The coupon is allowed to be used as many times as Sam wants. He ends up buying three books that all cost the same amount of money. The total cost for the books was \$45 . How much did each book cost, c , before the coupon was applied? |
Solution
First, let’s set up an equation that models the situation:
3(c - 5) = 45
Since each book costs the same amount, we denote this amount by the variable, c . Then we applied the \$5 coupon to each book, and finally, we will multiply the cost of each book after the coupon by 3 .
Now, simply solve for c like any other multi-step equation:
| 3(c) - 3(5) = 45 | Distribute the 3 |
| 3c - 15 = 45 | Simplify |
| 3c - 15 + 15 = 45 + 15 | Add 15 to both sides |
| 3c = 60 | Simplify |
| \dfrac{3c}{3} = \dfrac{60}{3} | Divide both sides by 3 |
| c = 20 | Solved |
Therefore, each book cost \$20 before the coupon was applied.
Keys to Remember: Solving Multi-Step Equations
- A multi-step equation is an equation that requires two or more steps to solve.
- When solving: remember whatever you do to one side, you must do to the other.
- To solve multi-step equations with fractions, you can multiply each term by the least common denominator to eliminate the fractions first.
- To check the solution, simply substitute the value into the variable to see if the equation is true.
- You can model real-life situations with an equation and solve for a correct solution.
Return to the Table of Contents








