What We Review
Introduction
Trigonometric equations and inequalities are essential topics for high school students tackling Precalculus and those preparing to study 3.10 Trigonometric Equations and Inequalities in AP® Precalculus. Understanding the process of solving trig equations not only aids in mathematical comprehension but also boosts problem-solving skills across various disciplines. This article explores trigonometric functions, equations, and inequalities, breaking them down into manageable segments with clear examples for easy understanding.
Understanding Trigonometric Functions
Trigonometric functions form the foundation of trigonometry. These include sine, cosine, and tangent, which are closely related to the unit circle—a circle with a radius of one. The unit circle helps describe how these functions behave, especially noting their periodicity. Periodicity means these functions repeat their values at regular intervals.
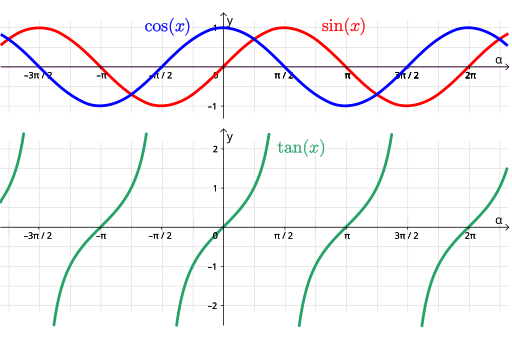
Example 1: Basic Function Values
To find basic function values like sine and cosine using the unit circle, consider an angle of 30^\circ.
- Step 1: Locate 30^\circ on the unit circle.
- Step 2: Understand that in the unit circle, sine corresponds to the y-coordinate, and cosine corresponds to the x-coordinate.
- Step 3: Read the coordinates: (\frac{\sqrt{3}}{2}, \frac{1}{2}) .
Therefore, \sin(30^\circ) = \frac{1}{2} and \cos(30^\circ) = \frac{\sqrt{3}}{2}.
Solving Trig Equations
A trigonometric equation is an equation involving trigonometric functions set equal to a value. Solving trig equations can involve inverse trigonometric functions and may require attention to domain restrictions.
Example 2: Solving a Simple Trigonometric Equation
Solve the equation: \sin(x) = 0.5
- Step 1: Use the inverse sine function to find x. This gives x = \sin^{-1}(0.5).
- Step 2: Calculate x. \sin^{-1}(0.5) = 30^\circ or \frac{\pi}{6} radians. However, we must use our knowledge of the unit circle as well to know that \sin x is also positive in Quadrant II and therefore \frac{5\pi}{6} is another valid solution
- Step 3: Consider the periodicity of sine. Sine repeats every 360^\circ or 2\pi. Thus, x = \frac{\pi}{6} + 2k\pi and x = \frac{5\pi}{6} + 2k\pi, where k is an integer.
Infinite Solutions and Periodicity
Trigonometric functions are periodic, which means solutions to trigonometric equations often repeat indefinitely. It is crucial to express these infinite solutions correctly.
Example 3: Finding All Solutions
Solve \tan(x) = 1.
- Step 1: Use the inverse tangent function: x = \tan^{-1}(1).
- Step 2: Calculate x. \tan^{-1}(1) = 45^\circ or \frac{\pi}{4}.
- Step 3: Tangent has a period of 180^\circ or \pi, so x = \frac{\pi}{4} + k\pi.
Solving Trigonometric Inequalities
Trigonometric inequalities involve expressions with greater than or less than symbols. Solving them requires methods like testing intervals or graphing the function.
Example 4: Solving a Trigonometric Inequality
Challenging Trigonometric Inequality Problem
Solve the inequality: 2\cos(x) + 1 \leq 0 for 0 \leq x < 2\pi
Step 1: Isolate the Trigonometric Function
Rearrange the inequality:
2\cos(x) \leq -1
\cos(x) \leq -\frac{1}{2}
Step 2: Determine Reference Angles
The reference angle for \cos^{-1} \left(\frac{1}{2}\right) is: \frac{\pi}{3}
Since \cos(x) is negative in quadrants II and III, the general solutions are:
x = \pi - \frac{\pi}{3}, \quad x = \pi + \frac{\pi}{3}
x = \frac{2\pi}{3}, \quad x = \frac{4\pi}{3}
Step 3: Express the Solution Set
Since we are looking for \cos(x) \leq -\frac{1}{2} , we include all x values in the intervals where cosine is less than or equal to -\frac{1}{2} , which are:
\frac{2\pi}{3} \leq x \leq \frac{4\pi}{3}
Thus, the solution is: \left[\frac{2\pi}{3}, \frac{4\pi}{3}\right]
Contextual Scenarios and Domain Restrictions
Real-world problems often impose domain restrictions. Understanding these contexts helps apply trigonometric solutions practically.
Example 5: Contextual Problem – Ferris Wheel Height Restriction
A Ferris wheel has a radius of 25 meters and takes 40 seconds to complete one full revolution. A rider’s height ( h(t) ) above the ground at time ( t ) (in seconds) is given by:
h(t) = 25\sin\left(\frac{\pi}{20} t - \frac{\pi}{2} \right) + 30
We want to find when the rider is at least 40 meters above the ground:
25\sin\left(\frac{\pi}{20} t - \frac{\pi}{2} \right) + 30 \geq 40
- Solve for ( t ):
25\sin\left(\frac{\pi}{20} t - \frac{\pi}{2} \right) \geq 10
\sin\left(\frac{\pi}{20} t - \frac{\pi}{2} \right) \geq \frac{2}{5} - Domain Restriction:
- Normally, this equation would have multiple solutions.
- However, since the Ferris wheel completes a cycle in 0 to 40 seconds, we only consider solutions in this time frame.
Thus, the real-world context limits the number of solutions compared to a general trigonometric equation.
Quick Reference Chart
| Vocabulary | Definition |
| Trigonometric Function | Functions like sine, cosine, and tangent used in trig equations. |
| Periodicity | The property of a trigonometric function to repeat its values in regular intervals. |
| Inverse Trigonometric Function | Functions that give the angle whose trigonometric function equals a given value. |
| Inequality | A mathematical statement that compares two expressions (e.g., >, <). |
| Solution Set | The set of all solutions to an equation or inequality. |
Conclusion
Mastering trigonometric equations and inequalities can seem daunting, but breaking the process into steps demystifies the topic. With practice, these concepts reinforce mathematical skills essential for AP® Precalculus and beyond.
Sharpen Your Skills for AP® Precalculus
Are you preparing for the AP® Precalculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!
Need help preparing for your AP® Precalculus exam?
Albert has hundreds of AP® Precalculus practice questions, free response, and an AP® Precalculus practice test to try out.









