Having grown up in the 21st century, you probably know that everything around you is fundamentally made of atoms. The chair you’re sitting on, the screen you’re looking at, and even the eyes you see with are made up of many different kinds of atoms. But what are atoms? What do they look like? And more importantly, how can you understand atomic structure for your AP® Chemistry Exam? In this Ultimate Guide, we’re going to give you a little bit of background on each topic to get you excited about it, and then we’re going to give you tips and advice on what you should memorize (or not), how to eliminate wrong answers quickly, and keywords that you should use in the long- and short-answer section of the exam.
We will first start our discussion with a brief overview of the wave-like nature electromagnetic radiation. We will then go on to discuss the particle-nature of matter and how the discoveries in the early 20th century shaped our understanding of the atomic structure and spectrum of the hydrogen atom. We’ll discuss Bohr’s model of the atomic structure of the hydrogen atom and the quantum mechanical model for atomic structure. We will dive into an explanation about the quantum numbers and their physical interpretations, and we will finish up this article with an overview of how atomic structure influences periodicity and periodic trends in the periodic table. Kapische? Let’s go!
Electromagnetic Radiation – Essential Knowledge 1.D.3
No discussion of atomic structure is complete without first understanding what electromagnetic radiation is. An example of electromagnetic radiation is the visible light that you see coming off your screen and hitting your eyes, giving objects color and visibility. Electromagnetic radiation also makes up the radio waves traveling to our cars and the Wi-Fi signal going to our phones and computers.

But clearly, there is a big difference between visible light and your Wi-Fi signal. What is that difference? All types of electromagnetic radiation can be described in terms of two variables: their wavelength and their frequency. Wavelength, denoted by the Greek letter lambda (\lambda) and measured in meters (\text{m}), is the distance between two peaks in a wave. Visible light is an example of short-wavelength electromagnetic radiation, with wavelengths between 400-700 \text{ nanometers (nm)}, or 1 billionth of a meter. Frequency, denoted by the Greek letter nu (\nu) and measured in Hertz (\text{Hz} = \text{s}^{-1}), is a measure of how many times per second the wave repeats itself. The higher the frequency of a wave, the higher the energy of the wave. An example you can relate to is that exposure to x-rays (\nu = 10^{18} \text{ Hz}) is much more harmful than exposure to FM radio waves (\nu = 10^{8} \text{ Hz}).
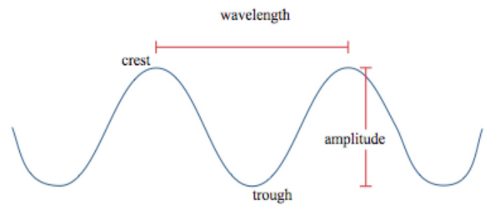
Another feature of electromagnetic radiation is that all electromagnetic waves travel at the speed of light (c= 2.998 \times 10^{8} \text{ m/s}). This means that the product of the wavelength and frequency of an electromagnetic wave are always equal to the speed of light, or:
c = \lambda \times \nu =2.998 \times 10^{8} \text{ m/s}
This equation will be given to you on the AP® exam, so there’s no reason to try and memorize it. It implies that frequency and wavelength are inversely proportional to each other, meaning that as one variable increases, the other decreases correspondingly. You should have no trouble solving this equation with a simple algebraic rearrangement of variables.
A great tip for quickly eliminating wrong answers on the multiple choice section and for checking your answers on the free response section is to focus on the exponents. Since the product of the variables must have an exponent of 10^{8} (the speed of light), it makes sense that if the known variable has a large positive exponent (e.g., \lambda = 8 \times 10^{15} \text{ m}), the corresponding variable must have a negative exponent (in this case, \nu = 3.75 \times 10^{-8} \text{ Hz}). This approach will help you instantly eliminate at least two wrong answers on the multiple choice section and will save you valuable time crunching numbers on the free response section.
This understanding of the relationship between frequency, wavelength, and the speed of light was one of the fundamental discoveries that paved the way towards an understanding of the atomic nature of matter. Now that we understand the wavelike nature of light, let’s move on the particle-like nature of light! Sounds crazy? You don’t even know!
Nature of Matter – Essential Knowledge 1.B.1, 1.D.3
Towards the end of the 19th century, a series of experiments were baffling physicists from around the world and challenging their understanding of the nature of matter. One of them was known as blackbody radiation. A blackbody is an idealized object that absorbs all incoming frequencies of electromagnetic radiation, approximated by a small slit in a large black box. A blackbody emits electromagnetic radiation at frequencies entirely based upon its temperature, and the classical model of light as waves was unable to account properly for the wavelengths of light being emitted!

To explain these results, German Physicist Max Planck (1858 – 1947), also known as the Father of Quantum Theory, theorized that, instead of matter being able to emit at infinite frequencies of electromagnetic radiation, there was some limit as to the frequency that light could be emitted or absorbed. In other words, he thought of the emission frequencies coming out of matter as a series of steps rather than a smooth ramp. For everyday objects, energy can take on any arbitrary value. However, Planck theorized that for small objects, the energy being emitted by objects was more like a staircase, where it could only come in discrete packets he called quanta. In other words, the energy released from objects is quantized, a phenomenon which eventually to what we know as the Quantum Theory of Matter. It turns out, the nature of matter is quantized! Planck, through mathematical derivation, arrived at what we now call Planck’s Constant (h), which is the smallest unit of energy that can be gained or lost by atoms, in units of Joules (energy) times second (time), where:
6.626 \times 10^{-34} \text{ J} \cdot \text{s}
This should seem strange – it’s like saying that a car can only travel at specific speeds! Even after his discovery, Planck was unconvinced that this constant was anything other than a theoretical mathematical artifact. It was, in fact, Albert Einstein (1879 – 1955) who was able to explain the importance of this discovery. Many people think that Einstein was given the Nobel Prize in Physics for his work on special relativity. In fact, Einstein was awarded the prize for figuring out the cause for the photoelectric effect. This effect was an experimental observation that, when you shone a light on a piece of metal hooked to a current meter, only electromagnetic waves above a certain frequency (regardless of the energy) cause electrons to be released from the surface of the metal.
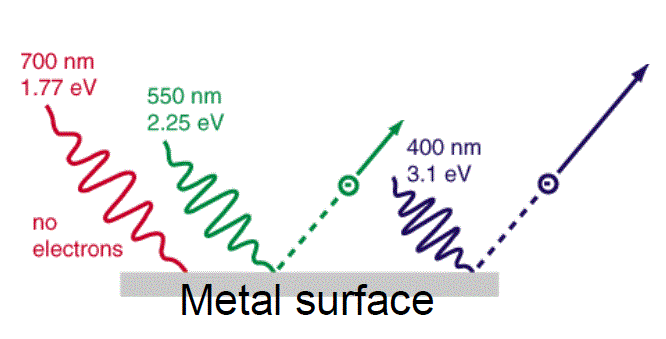
What made this observation even more interesting was that this was true regardless of the energy the light possessed. Einstein, using Planck’s Quantum Theory, hypothesized that the electromagnetic radiation hitting the metal was in fact composed of many small particles, which he called photons, and the energy of these photons was directly related to the frequency of the electromagnetic wave by the following relationship:
E_{photon} =h \nu \text{, where }h =6.626 \times 10^{-34} \text{ J} \cdot \text{s and the frequency is in units of Hz}
And using the previous relationship we learned about frequency and wavelength, this equation can also be interpreted as:
{ E }_{ photon }=h\nu =\dfrac { hc }{ \lambda}
The AP® exam will almost certainly contain some questions about this topic. So let’s review some common pitfalls.
Classic Expectation: A high enough intensity of light, regardless of frequency, should cause electrons to be ejected. Wrong!
Quantum Explanation: Light itself comes in little packets of energy called photons. At a specific wavelength, photons have a specific amount of energy, and only photons with enough energy, regardless of intensity, can knock out electrons.
Atomic Spectrum of Hydrogen – Essential Knowledge 1.D.3
The final experiment which demonstrated to physicists that the classical explanation of “electromagnetic radiation as waves” was incomplete was the atomic spectrum of hydrogen. If you put hydrogen gas in a tube and run a lot of electricity through it, it will emit light.

The classical explanation would predict that the light being emitted is a continuous spectrum containing all frequencies of light. However, that is not the case. Hydrogen emits light in what is called a line spectrum, meaning light is only emitted at discrete wavelengths.

Sound familiar? That’s because the quantum nature of matter can be used to explain the atomic spectrum of hydrogen! If we assume that hydrogen atoms can only emit photons of quantized energy, with the energy of each photon being:
{ E }_{ photon }=h n \nu
…where n is a positive integer value.
We find that the frequencies of emitted light exactly match those calculated by the equation! In fact, the integer n is our principal quantum number!
One thing to keep in mind is that on the AP® exam you may be given either frequency or wavelength for this calculation, so don’t forget to use the relationship previously discussed to convert between them.

Bohr Model – Science Practice 1.3, 3.3
The classical model of atomic structure assumes that the negatively-charged electrons orbit the positively charged nucleus at any arbitrary radius away from the nucleus, like planets in our solar system orbiting around the sun. Danish Physicist Niels Bohr (1885-1962) used the derivation of the principal quantum number of the hydrogen line spectra to revise this Classical Model of the Atom. He proposed that the electrons could only orbit the nucleus at discrete radii that he called shells, and electrons in shells further away from the nucleus possessed more energy. He proposed that the line spectrum of hydrogen was caused by the transition of electrons from one shell to another!

While this is certainly an attractive picture, these quantum calculations have shown us that this theory is in fact wrong! In Bohr’s model, electrons are still basically particles orbiting the nucleus. For various reasons we will not get into, this assumption simply cannot be true. In 1924, French Physicist Louis de Broglie presented his doctoral thesis (which was only two pages long!) proving that light, and in fact all particles, are inherently both particles and waves at the same time. This is known as wave-particle duality and was the breakthrough explanation necessary to explain how light, which clearly acts as a wave, can also act as a particle with quantized energy.
Quantum Mechanical Model of the Atom – 1.B.1, 1.C.2
This leads to a very strange implication: all objects are inherently fuzzy. And while macroscopic objects like cars have immeasurably small wavelengths, electrons have wavelengths that are measurable. It was for this reason that Erwin Schrödinger (1887 – 1961) proposed a series of mathematical equations called wave mechanics, which showed that all subatomic particles behave according to a set of quantum mathematical equations called wave functions. Rather than orbiting the nucleus in so-called planetary motion, electrons actually orbit the nucleus as an electron cloud. A feature of the electron cloud is that they are in fact areas of probability for locating electrons (the cutoff is 90% probability).

The Quantum Mechanical Model of the Atom treats all electrons as if they orbit the nucleus as a standing wave. An example of a standing wave is a guitar string, which, when plucked, vibrates at a certain harmonic frequency. In the same sense, electrons vibrate around the nucleus at a certain harmonic frequency. An important property of a standing wave is it does not propagate through space, and therefore, it must always equal a whole number integer such that the ends meet at both sides. Here are two visual examples: one of a string as a standing wave, the other of a circle as a standing wave.


In the second image on the right, we see an example of an impossible standing wave. It is impossible because only waves of certain frequencies match up correctly at each end, and form a complete circle.
Key Fact to Remember: It is these mathematically correct waves, known as harmonic frequencies, which correspond to the principal quantum number n previously discussed.
Quantum Numbers – Essential Knowledge 1.C.2
The quantum number n is one of four quantum numbers that are used to describe an electron in an atom. When given all four quantum numbers, we possess all the information necessary to describe atomic structure of an electron in an atom. The quantum numbers of an electron are the principal quantum number (n), quantum of angular momentum (l), the magnetic quantum number (m_l); and the spin quantum number (m_s ). Don’t get confused by the terminology. For the sake of the exam, try to keep things as simple as possible. You won’t be provided with any of this information explicitly, so it is important to understand this information as much as possible. Think about the flow from one quantum number to the next, and most importantly, don’t panic!
Table1. Quantum Numbers for each of the first four shells.
Quantum Numbers for the First Four Shells |
||||
n |
l |
Orbital Designation |
m_l |
Number of Orbitals |
| 1 | 0 | 1s | 0 | 1 |
| 2 | 0 | 2s | 0 | 1 |
| 1 | 2p | -1, 0, 1 | 3 | |
| 3 | 0 | 3s | 0 | 1 |
| 1 | 3p | -1, 0, 1 | 3 | |
| 2 | 3d | -2, -1, 0, 1, 2 | 5 | |
| 4 | 0 | 4s | 0 | 1 |
| 1 | 4p | -1, 0, 1 | 3 | |
| 2 | 4d | -2, -1, 0, 1, 2 | 5 | |
| 3 | 4f | -3, -2, -1, 0, 1, 2, 3 | 7 | |
The first quantum number, previously discussed, will tell you the harmonic wave function that corresponds to the electron, and it must be a positive integer value greater than zero. The greater n is, the greater the average radius of the electron is from the nucleus.
This has two important ramifications. First, the higher n is, the further away the electron is from the nucleus (i.e., the larger the circumference of its path), and the higher the energy of the electron is. Bigger n = Larger Energy. Second, the higher the quantum number, the less tightly bound the electron is, and the easier it is to be removed. That means that in an atom, electrons with the highest principal quantum number are the ones most likely to be knocked out of the atom first! This effect is due to the shielding of the electrons from the positive charge of the nucleus due to successive layers of electron shells, like magnets of like-pole repelling each other.
n = \text{Any Positive Integer } [1, 2, 3, …]
Angular momentum is a physical property that any orbiting object possesses. For a classical macroscopic object, angular momentum can take on any arbitrary value. However, as per the theme of this guide, electrons can only possess quantized angular momentum. The values of angular momentum that an electron may possess are entirely determined by the principal quantum number n of the electron.
\text{Possible values of Angular Momentum } (l): 0 < l < (n - 1)
Let’s look at an example.
If the electron of a hydrogen atom is in the first shell, what is its principal quantum number and what possible values of angular momentum can it possess?
In this example, the electron is in the first shell, meaning that n = 1.
For n = 1, 0 < l < [(1) -1] \rightarrow 0 < l < 0; in other words, l can only equal 0.
As you have probably seen before, each value of l corresponds to an orbital “name” given in the table below. It is important to remember these names!
Table 2. The given names of each of the common orbitals.
Angular Momentum Value (l) |
0 | 1 | 2 | 3 |
Given Name |
s | p | d | f |
The third quantum number is called the magnetic quantum number and is denoted m_l. The easiest way to think about this quantum number is to remember that it dictates Method of Leaning, or in regular English, the orientation of the orbital in space. Although the orientation doesn’t exactly depend on the value of m_l, for our purposes the comparison is sufficient. For example, while the s-orbital (m_l = 0) is spherical, meaning no orientation, the p-orbital (m_l=-1, 0, 1) is composed of three pairs of lobes, each of equal energy and oriented about one of the principal axes x, y, or z.

Electron Spin – Essential Knowledge 1.C.2
The final quantum number is called the electron spin and is denoted m_s. Let’s go back to the analogy of electrons as planets for a second. In this analogy, the electrons revolve around the nucleus, and the distance, speed, and direction of revolution are determined by the first three quantum numbers. However, there is another type of motion that the planet undergoes — rotation. The planet, or in this case the electron, rotates around itself. This rotation is an intrinsic property not just of electrons, but of all subatomic particles. Without getting into too many details, you’ll just have to accept it as a fact that the spin of all electrons is either pm \dfrac{1}{2}. The difference between positive and negative spin is akin to thinking about the earth either facing with the North Pole “up” or “down”. Let’s review the quantum numbers one more time before moving before moving on.
Table 3. A quick review of the quantum numbers and their meaning.
Symbol |
Quantum Number |
Explanation |
|
n |
Principal |
Determines electron energy and orbital size. |
|
l |
Angular Momentum |
Identifies orbital shape. |
|
m_l |
Magnetic |
Identifies orbital orientation. |
|
m_s |
Spin |
Identifies one of two possible spin states. |
Electron Configuration – Essential Knowledge 1.B.2, 1.C.1
As chemists, what we need to know is that no two electrons in an atom may have the same set of four quantum numbers. This means that only two electrons may occupy a given orbital (m_s=pm \dfrac{1}{2}). This concept is known as the Pauli Exclusion Principle. We denote the electron with the positive spin as an arrow facing up, and the electron with the negative as an arrow facing down. This is expressed visually as:

Electrons occupy the lowest-energy levels of an atom first. So, when trying to figure out the electron configuration of an atomic structure, we would fill out the lowest energy orbital (1s) before moving on to the next highest orbital (2s) and so on. This observation is known as the Aufbau Principle. Aufbau means “building up” in German, and it refers to the order in which we as chemistry students “build up” the electrons in an atomic structure. There are many mnemonic devices that help you memorize this diagram, but we find it easiest to memorize the exceptions rather than the rule:
3d is between 4s and 4p.
4d is between 5s and 5p.
For n = 6, the energy goes: 6s < 4f < 5d < 6p.
Another important thing to remember when applying the Aufbau principle is Hund’s Rule — that we obtain the lowest energy configuration of an atom by having the maximum number of unpaired electrons in so-called “degenerate” orbitals. Degenerate orbital is another word for orbitals of equal energy, i.e., the three 2p orbitals or the five 3d orbitals. So for an atom with enough electrons to fill five spots in the d-orbital (i.e., Manganese, atomic number 25), the lowest energy configuration would be to have each orbital with one electron.

With that, we have finished covering the general details of atomic structure! With the information provided hitherto, you should be able to answer any multiple choice question on the topic of atomic structure and to provide a reasonably detailed answer on the free response section. With this information at hand, we can now discuss periodic trends in the periodic table of the elements, whose conversation without this quantum knowledge would have been incomplete. Let’s begin with a quick historical conversation, and then move on the periodic table itself.
Periodicity – Essential Knowledge 1.C.1, 2.D.3
The science of chemistry emerged as an independent field of science after the experiments of French scientist Antoine Lavoisier (1743-1794), who is most famous for formulating the Law of Conservation of Mass. Among his less widely known accomplishments, however, was his discovery of the chemical constituents of the air, such as nitrogen and oxygen. His research on the elements paved the way for Russian chemist Dmitry Mendeleev (1834-1907), who discovered that if he rearranged the elements according to their mass, he was able to find similarities in their chemical properties. However, he couldn’t explain why this relationship existed.

We now know, however, that what he was seeing was the periodicity in the atomic structure of the elements. For example, all elements in the first column of the periodic table have one electron in their s-orbital. This electron configuration gives the atom certain chemical traits that are clearly distinguishable from chemicals in other columns of the periodic table. So what Mendeleev discovered was in fact that if we order the elements in order of their valence, or outermost, electrons, we discover elements with recurring chemical properties. This concept is known as periodicity, or periodic trends.
Periodic Trends – Essential Knowledge 1.C.1
There are other periodic trends besides chemical reactivity. The number and position of valence electrons determines the ionization energy (the energy required to remove an electron from an atom, or to ionize it into a +1 positive ion), the electron affinity (how attracted the element is to gaining another electron), atomic radius (the average radius of an atom, measured as half the distance between radii in a covalently bonded diatomic molecule), and metallic character (metals are solid and brittle, nonmetals are gaseous and pliable). The way these periodic trends play out are all neatly summarized in the image below:

You’ll have a periodic table on the AP® exam, and we’ve provided you with one here as well. The important thing is not to memorize exact examples, but rather to memorize trends. Now, let’s review some practice questions about periodicity.
Which element has a larger electron affinity: Fluorine or Cesium?
Fluorine (atomic number 7) is considered to be the element with the largest electron affinity. Cesium, on the other hand, is considered the element with the least electron affinity. Therefore, fluorine has the larger electron affinity.
Which element has a larger electron affinity: Iodine or Neon?
This is a trick question! Although you may think that Neon would have a higher electron affinity because it is further up and right of Iodine, in fact Neon is one of the noble gases. Noble gases are so-called because they have full valence electron shells. That means that they are highly non-reactive. It is in fact very tough to add or remove electrons from noble gases. Therefore, noble gases are less reactive than almost any other element.
Another note about noble gases: when writing out the valence electrons for an element, let’s say Manganese (Mn), you will often see this notation: [Ar]4s^23d^5. This notation is used to indicate that the element has the same electron configuration as Argon (Ar), plus seven electrons in the fourth shell. Argon, having a complete valence shell, has a complete electron configuration for the first three shells, or 1s^22s^22p^63s^23p^6. To save time writing these numbers out, chemists often write [Ar] to indicate those filled electron shells.

With that discussion about periodicity and periodic trends, we are done! By now you should be fully prepared to answer any question on the multiple choice or free response sections of your AP® Chemistry exam. Studying chemistry is not an easy task. It requires hours of preparation and study, and we have to understand material from a broad range of disciplines, such as biology, physics, and mathematics, to be good chemists. However, you should realize that the most exciting discoveries in pharmaceuticals, medicine, materials science, space flight, and more, are all possible due to chemists. Chemistry, after all, is the science of how all matter interacts with each other. And with the knowledge you have, you are prepared to enter an exciting world full of intrigue and discovery!
Did we miss anything? Do you have any questions about a topic we didn’t cover? Write us and we will be glad to explain further!
Good luck on your exam!
Looking for AP® Chemistry practice?
Kickstart your AP® Chemistry prep with Albert. Start your AP® exam prep today.








