Ultimate Guide to Stoichiometry Problems Introduction
Welcome to another chapter of the Ultimate Guide for AP® Chemistry! This time, we are going to discuss the topic of stoichiometry. Stoichiometry is the process by which we look at a chemical reaction, compare the products and reactants, and use the relationships established by the Law of Conservation of Mass and Energy to extract quantitative information. Stoichiometry allows us to find many useful things, including finding the limiting reagent in a reaction, how much of a product will be produced when a particular reaction takes place, and more. Let us go on a journey into quantitative chemistry!
- Law of Conservation of Mass
- Basics of Stoichiometry
- Balancing Chemical Reactions
- Solving Stoichiometric Problems
- Gas Laws
- Gas Pressure
- Gas Stoichiometry
- Oxidation States
- Balancing Redox Reactions
Law of Conservation of Mass – Essential Knowledge 1.E.2
The entire field of chemistry dates back to 1774 when French scientist Antoine Lavoisier published his treatise, “Traité Élémentaire de Chimie”, or Elementary Treatise of Chemistry. In it, he detailed his experiments on combustion of materials in air and formulated the Law of Conservation of Mass. This was a fundamental observation that paved the way towards stoichiometric analysis of chemical reactions in general. Shown below is a diagram of the sealed containers in which Lavoisier was able to establish that the materials gained in mass when burned in air.

The Law of Conservation of Mass, or Lavoisier’s Law, brings forth certain implications about quantitative chemistry. First of all, when we start a reaction with a defined amount of substance, and then when the reaction is finished with more mass is there than before, we know that more compound didn’t just appear from nowhere. Instead, we can assume that some particles from the air, like oxygen or water, combined with the reactant during the chemical reaction and formed a hybrid compound containing these extra atoms. This results in a higher mass.
Let us look at an example. What happens if we leave 10.00 \text{ g} of iron, Fe, in the air? After a month, the iron rusts solid, and when we weigh it again, we find that the mass of the oxidized iron is now 12.86 \text{ grams}! Where did the extra mass come from? This is a perfect Law of Conservation of Mass example. As you probably know, rusting is caused by the reaction of elemental iron with oxygen in the air to form rust. The reaction can be written out as:
Fe(s) + O_2(g) \rightarrow FeO (s)
The law of conservation of mass tells us that the additional mass must have come from the oxygen. Therefore, we can easily find the mass of oxygen by subtracting the initial mass of iron from the final mass of the rust. This lets us know how much oxygen combined with iron in this reaction. However, how would we predict the mass of rust resulting from the reaction of 10.00 \text{ grams} of iron with excess oxygen, without having to carry out the experiment? We do it based on stoichiometry.
Basics of Stoichiometry – Essential Knowledge 3.A.1, 3.A.2
The first thing we always do is use the molecular weight of an element to convert from the mass of the compound we have to the molar amount of it. A “mole” is a specific number of something — 6.022 \times 10^{23} of it, to be exact. Molar units are used extensively in chemistry as a way to deal with atoms and molecules, which there are billions of in even minute quantities of a substance. So, to convert from mass to a molar amount of particles (in units of moles), we add up the atomic masses of each element found in the periodic table, which is equivalent to the mass in grams per mole of substance, and then divide by the atomic or molecular weight of the substance. For our example, iron has an atomic mass of 55.85 \text{ g/mol}, so:
\dfrac{\text{Mass Iron}}{\text{Atomic Mass of Iron}} = \dfrac{10.00 \text{ g} }{55.85 \text{ g mol}^{-1}}= 0.1791 \text{ mol}
To not lose track of the units, we recommend using a table and crossing out the units to make sure you got it right at the end. To use this method, imagine that each column in the table is a fraction and that you have to multiply the numerator and denominator of all the fractions across. Units can cancel out if they appear once in the numerator and denominator. Using our example above:
10.00 \text{ g } Fe \times \dfrac{1 \text{ mol } Fe}{55.85 \text{ g } Fe} \times \dfrac{10.00 \times 1 \text{ mol}}{55.85} = 0.1791 \text{ mol}
This method of unit canceling is super useful for any algebraic calculations but is just especially appropriate for this one. Once we have the number of moles reacting, we can calculate the number of molecules of rust formed during the reaction. We do not need to know anything about the amount of oxygen being consumed! We can carry out the entire calculation based on the assumption that all of the iron reacts with oxygen to form rust. In other words, the number of iron atoms is equal to the number of rust molecules. We find the molecular weight of rust by adding together the atomic weights of iron and oxygen:
MW FeO = Fe + O = 55.85 \text{ g/mol} + 16.00 \text{ g/mol} = 71.85 \text{ g/mol}
10.00 \text{ g } Fe \times \dfrac{1 \text{ mol } Fe}{55.85 \text{ g } Fe} \times \dfrac{1 \text{ mol } FeO}{1 \text{ mol } Fe} \times \dfrac{71.85 \text{ g } FeO}{1 \text{ mol } FeO} \times \dfrac{10 \times 71.85 \text{ g } FeO}{55.85} = 12.86 \text{ g } FeO
One important note: recall that all quantitative calculations must be reported with the correct number of significant figures. The mass of iron was reported as 10.00, which contains four significant figures, so the final reporting number must also provide four significant figures. You may encounter questions on the multiple choice section of the AP® Exam that will trick you into a wrong answer by giving you the correct number but with the wrong number of significant figures. Make note of them as you go! And remember, when you multiply or divide, retain the same amount of significant figures as the number with the least significant figures.
What if I were to ask you how many molecules of oxygen were consumed during the reaction described above? To answer that question, you would have to balance the chemical reaction! Now we are going to move on to the topic of balancing chemical reactions.
Balancing Chemical Reactions – Essential Knowledge 3.A.1
The reaction described above, though correctly giving the reactants and products, remains unbalanced. That is because, if we look at it closely, the mass of all atoms on the right does not equal the mass of all atoms on the left. This reaction, therefore, violates the Law of Conservation of Mass and therefore is untrue. What we need to do to fix it is to make sure the number of same atoms is equal on both sides of the equation.
Fe(s) + O_2(g) \rightarrow FeO (s)
In this case, we need to add an oxygen atom on the left to balance out the molecular oxygen on the right. We do this by designating a coefficient in front of the product FeO, which indicates that two molecules of iron (II) oxide are formed by the reaction of iron and oxygen.
Fe(s) + O_2(g) \rightarrow 2FeO (s)
However, now we must balance the number of iron atoms on the right with the two iron atoms in iron (II) oxide. We do that by designating the coefficient ‘2’ in front of the elemental iron.
2Fe(s) + O_2(g) \rightarrow 2FeO (s)
The reaction is now completely balanced. From this information, we can stoichiometrically determine how much molecular oxygen is necessary for the complete oxidation of iron to iron (II) oxide.
Solving Stoichiometric Problems – Essential Knowledge 3.A.2
Example problem: Using the balanced equation from above, solve for the molar amount of oxygen consumed during the oxidation of 10.00 \text{ grams} of iron.
We will use the unit cancellation method described previously to address this problem. The key stoichiometric component is recognizing that for every two molecules of iron being consumed, one molecule of oxygen is consumed, and two molecules of rust are formed. Therefore, we can directly compare the amount of oxygen being consumed by using the balanced chemical reaction in the following manner:
10.00 \text{ g } Fe \times \dfrac{1 \text{ mol } Fe}{55.85 \text{ g } Fe} \times \dfrac{1 \text{ mol } O_2}{2 \text{ mol } Fe} \times \dfrac{10.00 \text{ mol } O_2}{55.85 \times 2} = 0.08953 \text{ mol } O_2
There will be many times where you will be given a concentration of a reagent in terms of its gas partial pressure, or be asked to solve a stoichiometric problem as it relates to the ideal gas law. We will, therefore, spend some time reviewing the ideal gas law and partial pressures and how they can be used in the context of stoichiometry.
Gas Laws – Essential Knowledge 2.A.2
After many experiments and scientific observations over the following hundred years, the collection of empirical gas evidence was compiled in one equation that related all the various properties of a gas to each other under ideal conditions. This equation is called the Ideal Gas Law.
PV = nRT, \text{ where } R = 0.08206 \dfrac{ \text{L atm} }{ \text{mol K} }
Pressure (P) is defined as the average force per unit area on a container. Atmospheric pressure, also known as standard pressure, is the force exerted by the air at sea level. It is the defined pressure under which ideal relationships are established. The temperature (T) of a gas is given in units of absolute temperature, the Kelvin scale (after Lord Kelvin). One unit of Kelvin is equal to one degree Celsius (1 \text{ K} = 1^\circ \text{C}).
Basically put, the product of the volume (V) and pressure (P) of an ideal gas, which are inversely proportional to each other, is equal to the product of the number of gas molecules (n, usually expressed in molar units) times the absolute temperature in Kelvin (T) times a constant of proportionality called the gas constant (R). The gas constant can be expressed in different units depending on what units the variables are reported on, but its function remains the same: to relate one side of the equation to the other. The number of gas molecules n can be readily converted to mass of particles by multiplying n by the molar mass of the molecule.
You can put down money that you will need to use Kelvin and Celsius together with stoichiometry! The biggest, most common mistake AP® Chemistry students make is trying to solve for a variable with units that do not match the gas constant. For example, if you wanted to solve for the pressure of a gas, and you were to input the pressure in degrees Celsius instead of Kelvin, your answer will be wrong. This can also happen if you were to input the pressure in units of Pascal instead of atmospheres, and forgot to change out the gas constant to reflect this change of units. The gas constant can be expressed in many different units, so just make sure that you have selected the version which matches the units in your equation. And don’t forget that sometimes the easiest thing to do is to convert your units rather than taking the time to find a new value of the gas constant.
Gas Pressure – Essential Knowledge 2.A.2, 4.A.1
According to the ideal gas law, pressure is related to the number of molecules of a gas. One derivation of this is that the total pressure of a gas is in fact composed of partial pressures of the different molecules that the gas consists of:
{ P }_{ total } = { P }_{ A } + { P }_{ B } + { P }_{ C } ...
A gas, like the air we breathe, consists of various constituent molecules of gas, such as carbon dioxide (CO_2), nitrogen (N_2), oxygen (O_2), and water (H_2O). Even though the air, in general, has a total pressure, we can measure the contribution of the partial pressure of each type of gas molecule to the total pressure. This relationship is another consequence of the kinetic theory of gases: considering that it is the collisions of each molecule of gas with the wall of the container that provide the total pressure, the amount of pressure exerted by each gas individually is directly proportional to the sum of that particular gas inside the container. This quantity is known as the molar fraction.
{ P }_{ A } = { P }_{ total } \times { X }_{ A }, \text{ where } { X }_{ A } = \dfrac { \text{moles } A }{ \text{total moles} }
Gas Stoichiometry – Essential Knowledge 3.A.2
In the next section, we will discuss how to balance gaseous reactions stoichiometrically. The concentration of a gas is usually expressed in terms of its partial pressure. Let’s give an example:
{ O }_{ 2 }(g) + { C }_{ 6 }{ H }_{ 12 }{ O }_{ 6 }(s) = { CO }_{ 2 }(g) + { H }_{ 2 }O(g) + q
Above is the unbalanced reaction for the combustion of glucose in oxygen to water and carbon dioxide. As you can see, all the compounds besides glucose are gases. Balancing this reaction is no different than balancing any other reactions: we place the compounds side by side, determine how many moles of each reactant would be required for the reaction to go to completion, and how many moles of the product would be generated. In this case, we know that carbon-containing products will be produced in multiples of six, and hydrogen-containing products in multiples of twelve. Using the lowest-possible multiple, we find that the reaction balances to:
6{ O }_{ 2 }(g) + { C }_{ 6 }{ H }_{ 12 }{ O }_{ 6 }(s) = { 6CO }_{ 2 }(g) + 6{ H }_{ 2 }O(g) + q
In our next section, we will approach the topic of electrochemistry and how to stoichiometrically balance redox reactions. However, before doing that, it is important that we review how to assign oxidation states to the molecules in a reaction.
Oxidation States – Essential Knowledge 3.B.3
Assigning oxidation number can be a big issue for many students because there are millions of chemical compounds each with their own identities. The information overload can cause you to panic, especially during the AP® exam when it is more crucial for you to stay calm. So we’re going to teach you a great method to remember how to assign oxidation states that you’ll be able to use on the AP® Exam. It involves using the periodic table, which you get for free!
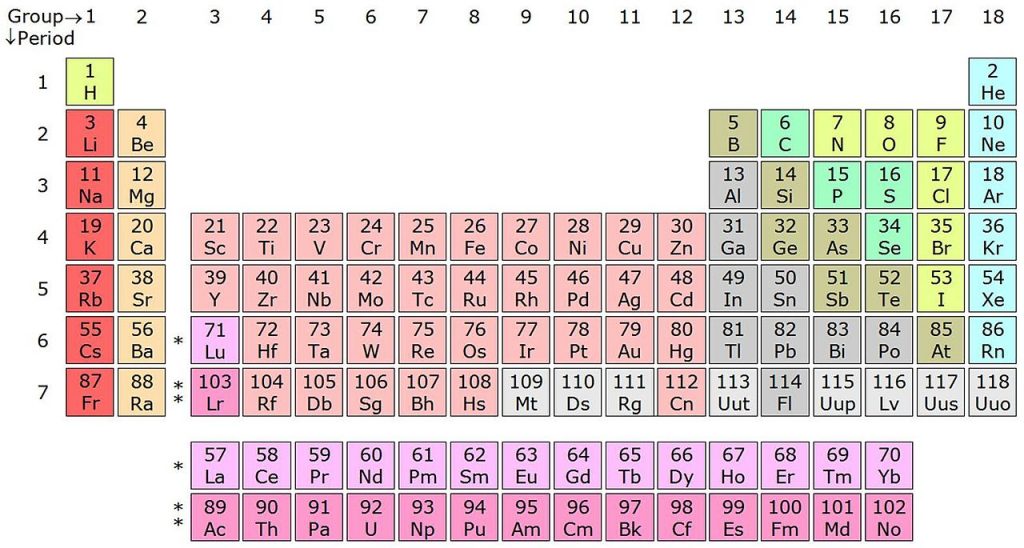
Oxidation state relates to electronegativity, and it also relates to electron configuration. Therefore, think about the periodic table when we go through these rules, and memorize them in terms of the table. When you finish applying these rules, assign the remaining oxidation states in the compound by keeping in mind that the sum of all oxidation state numbers must equal the net charge on the molecule.
| Rule Number | Chemical Species | Oxidation State | Exceptions |
| 1 | Elemental Form | 0 | |
| 2 | Monoatomic Ions | Ionic Charge | |
| 3 | Group 1A,2A Metals | +1, +2 | |
| 4 | Oxygen | -2 | Except in peroxides and F_2O |
| 5 | Hydrogen | +1 | Except in metal hydrides where it is -1 |
| 6 | Fluorine | -1 | |
| 7 | Chlorine, Bromine, Iodine | -1 | Except in compounds with O or F |
| 8 | Groups 7A, 6A, 5A | -1, -2, -3 | *in binary compounds with metals |
So what do we mean when we say “keep the periodic table in mind”? Let’s take a look at Rule 3: “Group 1A, 2A Metals – +1, +2”. The reason for this rule is that alkali and alkaline earth metals are much more stable without any electrons in their outlying s-orbital, and they tend to lose those electrons to form more stable ions. Looking at the periodic table shows you this relationship visually. In the ground state, those metals will have outlying electrons, which is energetically unfavorable. The same line of reasons can be used for Rules 6 and 8, where we can see how the position of these elements can affect the number of electrons they lose to become stable.
Rule 7 makes sense when considering the difference in electronegativities between the halogens (Group 7A). Electronegativity decreases as you go down a group, and the most electronegative atoms are assigned the negative oxidation state. Since fluorine is the most electronegative element, followed by oxygen, any compounds formed between fluorine/oxygen and another halogen will cause a positive oxidation state to be placed on the halogen. In every other case, however, the halogens will be the most electronegative atoms, so they will have an oxidation state of -1.
So, apply the rules, then assign the remaining oxidation states based on “the sum of oxidation states equals the net charge”. Let’s practice assigning oxidation numbers to our rusting iron example. The balanced chemical reaction is:
4Fe(s) + 3O_2(g) = 2Fe_2O_2(s)
Rule 1: Fe(s) and O_2(g) have an oxidation state of 0.
Rule 4: Oxygen’s oxidation state is -2.
To get the oxidation state of Fe, get the total number of atoms of each element in the compound and balance it to equal the net charge on the compound.
We’re done! You now possess all the knowledge necessary to assign oxidation states correctly. Armed with this knowledge, we will now balance the redox reaction of iron rusting and generalize that example to balancing redox equations in general.
Balancing Redox Equations – Essential Knowledge 3.B.3, 3.C.3, 6.A.1
Since we now know the oxidation states of the products and reactants, we can split the balanced reaction up into its constituent oxidation and reduction reactions. You designate the oxidation state by writing it as if it were an electric charge on the element. The balanced oxidation half-reaction would look like this:
4Fe(s) = 4Fe^{3+} \quad Fe(s) = Fe^{3+}
And the balanced reduction half-reaction would look like this:
3O_2(g) = 6O^{2-} \quad O_2(g) = 2O^{2-}
The same rules for balancing the electric charge across the reaction apply to half-reactions as well. Once oxidized, iron has an oxidation state of 3+. We indicate that the iron atom loses three electrons to balance this positive charge. This is written as:
Fe(s) =Fe^{3+} + 3e^{-}
Now the net charge on both sides of the equation is zero, and the reaction is balanced. The reduction half-reaction would look like this once accounting for the electrons:
4e^{-} + O_2(g) = 2O^{2-}
Notice that we wrote the electrons on the reactant side of the equation in this case to balance it out, because it was the products that had the charge on them. This is generally the case for reduction half-reactions.

We now have the two balanced half-reactions rusting. What do we do with this information? Well, we now add the two reactions together and balance that! The goal here is to multiply each half-reaction by the least common denominator of the electrons on each side, so that when we add the reactions together, the electrons cancel out.
4 \times [Fe(s)] = [Fe^{3+} + 3e^-] \times 4
3 \times [4e^- + O_2(g)] = [2 O^{2-}] \times 3
4Fe(s) = 4Fe^{3+} + 12e^-
12e^- + 3O_2(g) = 6O^{2-}
4Fe(s) + 3O_2(g) = 4Fe^{3+} + 6O^{2-} = 2Fe_2O_3
The final product of this reaction, Fe_2O_3(s), or Iron (III) Oxide, is rust. There are other electrochemical reactions that, besides electrons, also produce protons (H^+), which you also have to balance until they cancel out, but we won’t get into that right now. Let us look at the process one more time step-by-step to make sure we got it right.
- Balance the chemical reaction.
- Assign oxidation states to all elements.
- Write out the two redox half reactions.
- Balance the charge on each half-reaction by adding electrons.
- Add the two half-reactions together to arrive at your final balanced electrochemical reaction.
Otherwise, solving redox stoichiometry reactions is the same as other stoichiometry problems! Balance the reaction, and use unit conversion to solve the preferred question.
This wraps up the topic of stoichiometry! There are a million different examples of stoichiometric problems to practice on, and we wholeheartedly recommend that you attempt to review all of them! Start with the answers to Part A in the 2015 AP® Chemistry Question 2. And make up your own! Soon enough you will master the topic by yourself, and then you will be teaching your friends! So take your knowledge, and good luck!
Looking for AP® Chemistry practice?
Kickstart your AP® Chemistry prep with Albert. Start your AP® exam prep today.








