Introduction
The Fundamental Theorem of Calculus brings together two essential concepts in calculus: differentiation and integration. There are two parts to the Fundamental Theorem: the first justifies the procedure for evaluating definite integrals, and the second establishes the relationship between differentiation and integration. Here, we will focus on the first statement, which is referred to as the First Fundamental Theorem of Calculus.
This theorem establishes the procedure for computing a definite integral. Recall that a definite integral is an integral where you are given the limits of integration. That is, you are integrating over an interval whose endpoints you use to evaluate the integral.
Indefinite vs. Definite Integrals
An indefinite integral is an integral without limits of integration; for example,
\int { { x }^{ 2 } } dx
When integrating this function, we are looking for a curve whose derivative is {x}^{2}. There are infinitely many curves with that derivative, including
\dfrac { 1 }{ 3 } { x }^{ 3 }
\dfrac { 1 }{ 3 } { x }^{ 3 }+1
\dfrac { 1 }{ 3 } { x }^{ 3 }+8
\dfrac { 1 }{ 3 } { x }^{ 3 }-3
\dfrac { 1 }{ 3 } { x }^{ 3 }-\sqrt { 5 }
While there are infinitely many options, we note that they differ only by a constant. As a result, when we integrate a function of this type, we add an arbitrary constant, C, to our solution, as follows:
\int { { x }^{ 2 } } =\dfrac { 1 }{ 3 } { x }^{ 3 }+C
In contrast, a definite integral is one in which there are limits of integration. As an example, consider \int _{ 1 }^{ 4 }{ { x }^{ 2 } dx } . Here, we are being asked to integrate the same function as before, but we are doing so over the interval 1\le x\le 4. To compute this integral, we rely on the First Fundamental Theorem of Calculus.
The First Fundamental Theorem of Calculus
The theorem states that if a function f(x) has an indefinite integral of F(x)+C and is continuous over an interval [a,b], then \int _{ a }^{ b }{ f(x)dx=F(b)-F(a) }.
Let’s go back to our prior example:
\int _{ 1 }^{ 4 }{ { x }^{ 2 } dx }
First, we integrate { x }^{ 2 } to obtain \dfrac { 1 }{ 3 } { x }^{ 3 } . When evaluating definite integrals, we leave out the constant (so there is no +C here).
Next, we plug the limits of integration into the integral we just found. We first evaluate the upper limit of integration (F(b)), then subtract the value of the function at the lower limit of integration (F(a)). Putting this all together, we obtain the following expression:
\int _{ 1 }^{ 4 }{ { x }^{ 2 } dx } =\dfrac{x^3}{3} \int_{1}^{4}=\dfrac { 1 }{ 3 } { (4) }^{ 3 }-\dfrac { 1 }{ 3 } { (1) }^{ 3 }=\dfrac { 1 }{ 3 } (64-1)=\dfrac { 1 }{ 3 } (63)=21
Why does it Work?
Let G(x)=\int _{ a }^{ x }{ f(t)dt } .
We can show that F(x) is an antiderivative for f on some interval [a,b]. This result is actually because of the Second Fundamental Theorem of Calculus. We can show that the second fundamental theorem works without using the first, but interestingly, proving the first part is easiest if we start with the second part.
The two anti-derivatives are continuous over the given interval. Also, { G }^{ ' }(x)={ F }^{ ' }(x)=f(x) for all x in the interval [a,b] . In other words, since G(x) and F(x) are anti-derivatives of f(x), their derivative is f(x).
You might remember that a function has multiple anti-derivatives and that these differ by a constant. This is why you add +C at the end of your answers when you evaluate an indefinite integral (one without limits of integration). As a result, we know there exists another anti-derivative of f on some interval [a,b]. Let us call this anti-derivative F(x), where G(x)=F(x)+C.
Recall that G(a)=\int _{ a }^{ a }{ f(t)dt=0 }. That is, the integral at a particular point within the interval is equal to zero. From this statement, we arrive at the following:
0=G(a)=F(a)+C
C=-F(a)
We noted before that G(x)=F(x)+C. Since we just found a value for C, we have
G(x)=F(b)-F(a).
If we let x=b, we arrive at G(b)=F(b)-F(a). Using the relationship between anti-derivatives and derivatives, we conclude that
\int _{ a }^{ b }{ f(t)dt=F(b)-F(a) }.
Example 1:
Find \int _{ 0 }^{ \pi /2 }{ cos(x)dx }.
In this straightforward example, we are asked to evaluate a definite integral. Recall that the derivative of sin { x } is cos { x }, so the anti-derivative of cos { x } is sin { x } + C. However, as this is a definite integral (i.e. we are given the limits of integration), we need not add the constant (C). We evaluate the integral by using the first fundamental theorem as follows:
\int _{ 0 }^{ \pi /2 }{ cos { x }dx } =sin{x} \int_{0}^{\pi/2}= sin { (\pi /2) } - sin { (0) } =1-0=1
Example 2: (1988 AP® Calculus Exam Multiple Choice Problem 10)
If \int _{ 0 }^{ k }{ (2kx-{ x }^{ 2 })dx=18 } what is the value of k?
Here, we have removed the multiple choice answers, but the question is identical to one that appeared on the AP® exam in all other respects.
We are asked to find k, which involves evaluating the given definite integral. Invoking the first fundamental theorem of calculus, we know that we must find the difference between the values of the anti-derivative at k and at 0.
Keep in mind that k is a constant (a number), as this will help us with the anti-derivative. Specifically, when finding the anti-derivative of 2kx, we treat k as we might the number 2. That is, we leave it alone! It is not a variable and so there should be no \dfrac { { k }^{ 2 } }{ 2 } anywhere in your work!
We find the anti-derivative as follows:
\int _{ 0 }^{ k }{ (2kx-{ x }^{ 2 })dx } =\dfrac{2kx^2}{2}-\dfrac{\pi^3}{3} \int_{0}^{k}=kx^2-\dfrac{x^3}{3} \int_{0}^{k}=\dfrac{3kx^2}{3}-\dfrac{x^3}{3} \int_{0}^{k}=\dfrac{3kx^2-x^3}{3} \int_{0}^{k}
Now, we apply the Fundamental Theorem of Calculus. This means that we evaluate the definite integral by using the limits of integration (first substituting k for x, then 0 for x) as follows.
\dfrac{3kx^2-x^3}{3} \int_{0}^{k}=\dfrac { 3k \cdot { k }^{ 2 }-{ k }^{ 3 } }{ 3 } -\dfrac { 3k{ (0) }^{ 2 }-{ (0) }^{ 3 } }{ 3 } =\dfrac { 3{ k }^{ 3 }-{ k }^{ 3 } }{ 3 } -0=\dfrac { 2{ k }^{ 3 } }{ 3 }
Recall that
\int _{ 0 }^{ k }{ (2kx-{ x }^{ 2 })dx=18 }. Thus, \dfrac { 2{ k }^{ 3 } }{ 3 } =18 and { k }^{ 3 }=\dfrac{\left(18\cdot3\right)}{2}=27
k=3
Example 3: (1988 AP® Calculus Exam Multiple Choice Problem 13)
If the function f has a continuous derivative on [0,C] then \int _{ 0 }^{ c }{ { f }^{ ' }(x)dx=? }
- f(c)-f(0)
- | f(c)-f(0) |
- f(c)
- f(x)+C
- { f }^{ " }(c)-{ f }^{ " }(0)
This problem is testing us on our understanding of the Fundamental Theorem of Calculus. The anti-derivative of the derivative of f is f itself. Next, we evaluate the definite integral by using the limits of integration. The answer is (A).
What does \int _{ a }^{ b }{ f(t)dt=F(b)-F(a) } actually mean?
We can understand the integral \int _{ a }^{ b }{ f(t) } dt in a number of ways. One of these is to think of the integral as the total change in the curve over the interval from a to b. The total change is the definite integral of the rate of change of a function. Below are some questions from actual AP® Calculus exams that require the use of the First Fundamental Theorem of Calculus and the fact that the definite integral gives the total change of the function over the given integral.
Example: (2007 AP® Calculus AB Exam Question 2 part b)
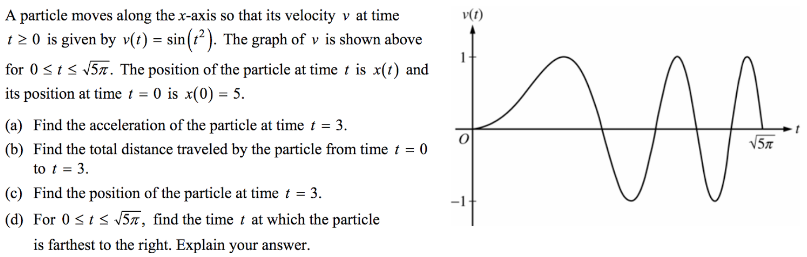
We will focus on part b and note that we are asked for the total distance that the particle traveled between t=0 and t=3. We can integrate the given velocity function to arrive at the position function. However, the distance traveled is irrespective of direction, so we must remember to take the absolute value of the velocity first.
The total distance traveled can be found using a definite integral. Namely, \int_{0}^{3} sin(t^2)dt=1.702
Example 5: (2007 AP® Calculus AB Form B Exam Question 2 part a)

We are asked for the total water entering the tank between t=0 and t=7. The rate of water entering the tank is f(t) and the total amount of water entering the tank can be found using a definite integral:
\int _{ 0 }^{ 7 }{ f(t) } dt=8264 gallons.
The Fundamental Theorem of Calculus
As you can see, the fundamental theorem of calculus establishes a procedure for calculating a definite integral. Now, this theorem on its own is already useful, but it also supplies us with the fact that this definite integral is equivalent to the total change over a particular interval, which comes in handy in a number of situations as we saw in the last two problems above.
Looking for AP® Calculus practice?
Kickstart your AP® Calculus prep with Albert. Start your AP® exam prep today.








