What We Review
Introduction
Section 2.8 Inverse functions is a fundamental chapter in precalculus. They allow us to reverse a function’s operation, making them essential for problem-solving. Grasping inverse functions and the inverse graph is crucial, especially for the AP® Precalculus exam, where understanding these concepts can significantly boost your performance.
What Is an Inverse Function?
An inverse function, denoted as f^{-1}(x), essentially undoes what the original function, f(x), does. If f(x) takes a to b, then f^{-1}(x) will take b back to a. In simpler terms, inverse functions reverse the roles of inputs and outputs.
Key properties of inverse functions include:
- The combination, or composition, of a function and its inverse results in an identity: f(f^{-1}(x)) = x.
- When graphed, the inverse is a reflection over the line y = x, known as the identity function.
How to Determine If a Function Is Invertible
Not all functions have inverses. A function must meet certain criteria to be invertible:
- One-to-One Correspondence: Each input corresponds to only one output, and each output corresponds to only one input. This implies the function must pass the horizontal line test on its graph.
Example 1: Checking Invertibility
Consider the function f(x) = x^2. Is it invertible?
- Graph It: Plot the graph of f(x) = x^2. Observe that it is a parabola opening upwards.
- Horizontal Line Test: Draw horizontal lines across the graph. Notice they intersect the parabola at two points, indicating more than one input yields the same output.
- Conclusion: Therefore, f(x) = x^2 is not invertible across all real numbers since it fails the horizontal line test.
Finding the Inverse of a Function
To find a function’s inverse, follow these steps:
- Replace: Change f(x) to y.
- Swap and Solve: Swap x and y, then solve for y.
Example 2: Finding the Inverse
Find the inverse of f(x) = 2x + 3.
- Replace and Swap: Start with y = 2x + 3. Switch x and y to get x = 2y + 3.
- Solve for y: Rearrange to find y. Subtract 3: x - 3 = 2y, then divide by 2: y = \frac{x - 3}{2}.
- Inverse Function: Thus, the inverse is f^{-1}(x) = \frac{x - 3}{2}.
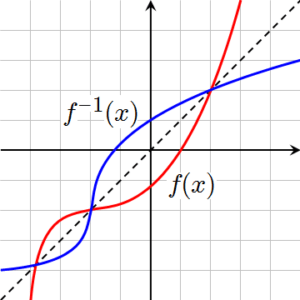
Graphing Inverse Functions
Let’s talk about how to graph inverse functions. Graphing the inverse involves reflecting the original function graph over the line y = x, which is the identity function. This reflection helps visualize how the inverse function interchanges the roles of inputs and outputs.
Example 3: Graphing an Inverse Function
Given f(x) = \frac{1}{3}x - 2 , graph its inverse.
- Find the Inverse: From above, the inverse is f^{-1}(x) = 3x+6 .
- Plot Original and Inverse: Graph \frac{1}{3}x - 2 and f^{-1}(x) = 3x+6.
- Reflect Over y = x: Observe how f(x) and f^{-1}(x) are reflections over y = x.
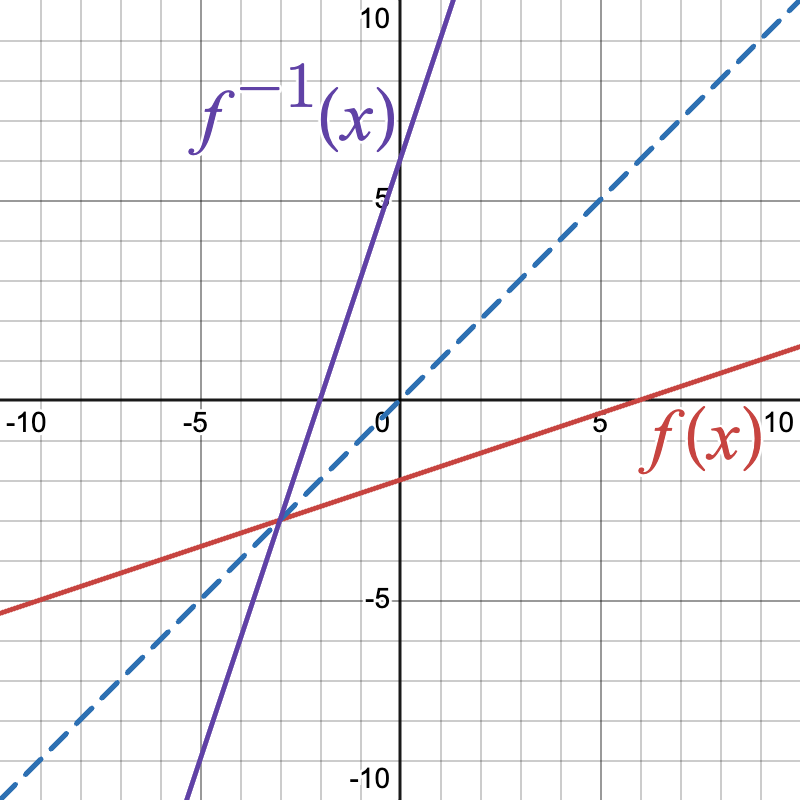
Vocabulary Quick Reference Chart
| Term | Definition |
| Inverse Function | A function that reverses the mapping of the original function. |
| Invertible Function | A function with a unique output for every input and can have an inverse. |
| Identity Function | A function defined by h(x) = x that reflects points graphically. |
| Composition | Combination of two functions; f(f^{-1}(x)) = x indicates invertibility. |
Additional Considerations
Real-world problems often rely on inverse functions to reverse operations. In fields like finance and engineering, such applications can solve complex equations or predict outcomes based on initial conditions.
Conclusion
Inverse functions and their graphical representations are indispensable tools in mathematics. Mastering these concepts allows for greater mathematical flexibility and prepares you well for the AP® Precalculus exam.
Sharpen Your Skills for AP® Precalculus
Are you preparing for the AP® Precalculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!
Need help preparing for your AP® Precalculus exam?
Albert has hundreds of AP® Precalculus practice questions, free responses, and an AP® Precalculus practice test to try out.









